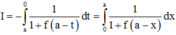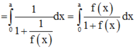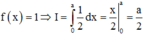Tính tích phân I = ∫ 0 1 ( x - 3 ) 8 ( 2 x + 1 ) 10 d x ta được
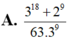
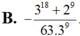
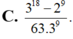
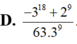
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Tính tích phân : \(I=\int\limits_{\frac{-1}{2}}^0\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}\)
\(I=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\left(\sqrt{\left(x+1\right)\left(3-x\right)}\right)}\)
\(=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)^2\sqrt{\frac{3-x}{x+1}}}\)
Đặt \(t=\sqrt{\frac{3-x}{x+1}}\Rightarrow\frac{dx}{\left(x+1\right)^2}=-\frac{1}{2}\)
Đổi cận : \(x=-\frac{1}{2}\Rightarrow t=\sqrt{7};x=0\Rightarrow t=\sqrt{3}\)
\(I=-\frac{1}{2}\int\limits^{\sqrt{3}}_{\sqrt{7}}dt=\frac{1}{2}\left(\sqrt{7}-\sqrt{3}\right)\)
Cho hàm số y = f x = x 2 k h i 0 ≤ x ≤ 2 - x k h i 1 ≤ x ≤
Tính tích phân I = ∫ 0 2 f x d x
A. 5 6
B. 1 3
C. 2
D. 3
Cho hàm số y = f ( x ) = x 2 k h i 0 ≤ x ≤ 1 2 - x k h i 1 ≤ x ≤ 2
Tính tích phân I= ∫ 0 2 f ( x ) d x
![]()
![]()
![]()
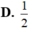
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân I = ∫ 0 1 f ' x d x
A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.
Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
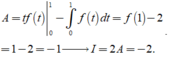
Cho hàm số y = f(x) xác định và liên tục trên 0 ; + ∞ sao cho x 2 + x . f e x + f e x = 1 với mọi x ∈ 0 ; + ∞ Tính tích phân I = ∫ e e ln x . f ( x ) x d x .
A. I = - 1 8 .
B. I = - 2 3 .
C. I = 1 12 .
D. I = 3 8 .
Đáp án C
Phương pháp:
Đặt ẩn phụ t = ln x.
Cách giải:
Ta có:
![]()
![]()
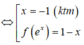
Đặt
![]()
Khi đó :
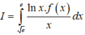
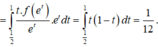
Cho hàm số y=f(x) xác định và liên tục trên 0 ; + ∞ sao cho x2+ x.f(ex) + f(ex)=1 với mọi x ∈ 0 ; + ∞ . Tính tích phân I = ∫ e e ln x . f ( x ) x d x
A. -1/8
B. -2/3
C. 1/12
D. 3/8
Cho số thực a > 0. Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f x . f a − x = 1. Tính tích phân I = ∫ 0 a 1 1 + f x d x
A. I = a 3
B. I = a 2
C. I = a
D. I = 2 a 3
Đáp án B
I = ∫ 0 a 1 1 + f x d x = ∫ 0 a d x 1 + 1 f a − x = ∫ 0 a f a − x 1 + f a − x d x
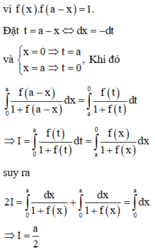
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận 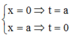
=>