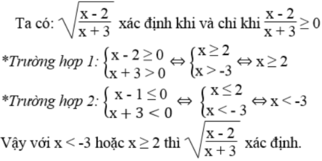biểu thức căn bặc hai của 2x+3 xác định khi nào

Những câu hỏi liên quan
Giúp mình bài này với
Cho hai đa thức sau P(x)=x ^3- 2x ^2 + x-2; Q(x)=2x^3-4x^2+3x-6
a, Tính M(x)=P(x)-Q(x) Xác định bặc hệ số cao nhắt hệ số tự do của đa thức M(x)
b. Chứng tỏ rằng x=2 là nhiệm của hai đa thức P(x)-Q(x)
tìm điều kiện xác định của các biểu thức sau :
a, căn của 3/4 -5x
2, căn của -3/1-2x
a )
\(\sqrt{\frac{3}{4}-5x}\ge0\)
\(< =>\frac{3}{4}-5x\ge0\)
\(< =>-5x\ge-\frac{3}{4}\)
\(< =>\frac{-20x}{4}\ge-\frac{3}{4}\)
\(< =>-20x\ge-3\)
\(< =>x\ge\frac{3}{20}\)
\(\sqrt{\frac{-3}{1}-2x}\ge0\)
\(< =>-3-2x\ge0\)
\(< =>-2x\ge3\)
\(< =>x\ge-\frac{3}{2}\)
Đúng 0
Bình luận (0)
Tìm điều kiện để các biểu thức sau xác định
a) căn bậc hai của 2x+4/x^2-6x+9
b) căn bậc hai của x^2+2x+3
Mng giúp em vs ak thanks
cho biểu thức B=[ x+1/ 2x-2 +3/x2 -1 -x+3/2x+2] .2x2 -2/5
a, tìm điều kiện của biến để phân thức xác định
b, c/m rằng khi giá trị của biểu thức xác định thì nó không phụ thuộc vào biến x ?
Biểu thức
3
-
2
x
xác định khi: A.
x
3
2
B.
x
3
2
C.
x
≥
3
2
D.
x
≤
3
2
Đọc tiếp
Biểu thức 3 - 2 x xác định khi:
A. x > 3 2
B. x < 3 2
C. x ≥ 3 2
D. x ≤ 3 2
cho biểu thức A = (2 căn x +x chia x căn x -1 -1 chia căn x - 1 ) chia ( căn x + 2 chia x + căn x +1 )
a) tìm điều kiện xác định của biểu thức A
b) rút gọn biểu thức A
c) tính giá trị A khi x = 9-4 căn 5
d) tìm giá trị lớn nhất của A
a: ĐKXĐ: x>=0; x<>1
b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)
d: căn x+2>=2
=>A<=1/2
Dấu = xảy ra khi x=0
Đúng 1
Bình luận (0)
Biểu thức sau đây xác định với giá trị nào của x?
x - 2 x + 3
Cm bất đẳng thức :
Căn bậc hai ab >HOặc= căn bặc hai c(a-c)+ căn bậc hai c(b-c)
Tìm điều kiện xác định của mỗi biểu thức
a)căn(x^2-3x+2)
b)căn(2x^2+4x+5)
g)căn(x^2+4x+5)
Bài làm:
a) \(\sqrt{x^2-3x+2}=\sqrt{\left(x-1\right)\left(x-2\right)}\)
Ta xét 2 trường hợp sau:
Nếu: \(\hept{\begin{cases}x-1\ge0\\x-2\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge1\\x\ge2\end{cases}\Rightarrow}}x\ge2\)
Nếu: \(\hept{\begin{cases}x-2\le0\\x-1\le0\end{cases}\Rightarrow}\hept{\begin{cases}x\le2\\x\le1\end{cases}\Rightarrow}x\le1\)
Vậy \(\orbr{\begin{cases}x\ge2\\x\le1\end{cases}}\)
b) \(\sqrt{2x^2+4x+5}=\sqrt{\left(x+2\right)^2+x^2+1}\)
Mà \(\left(x+2\right)^2+x^2+1>0\left(\forall x\right)\)
Vậy biểu thức xác đinh với mọi x
c) \(\sqrt{x^2+4x+5}=\sqrt{\left(x+2\right)^2+1}\)
Mà \(\left(x+2\right)^2+1>0\left(\forall x\right)\)
Vậy biểu thức xác định với mọi x
Học tốt!!!!