tính diện tích còn lại

Những câu hỏi liên quan
Câu 1: a) Tính diện tích hình thoi có độ dài hai đường chéo là 5cm và 7cm. b) Tính diện tích hình thang có độ dài hai đáy là 4cm và 6cm, đường cao 3cm c) Tính diện tích hình bình hành có độ dài đáy là 8cm và đường cao ứng với cạnh đáy đó là 7cm Câu 2: Viết tỉ số của cặp đoạn thẳng có độ dài như sau:AB 7cm và CD 14cm Câu 3: a) Cho D ABC ∽ D MNI. BiếtAˆA^ 800;NˆN^ 300. TínhCˆC^ b) Cho DABD DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. Câu 4: Cho tam giác ABC có AB 4...
Đọc tiếp
Câu 1:
a) Tính diện tích hình thoi có độ dài hai đường chéo là 5cm và 7cm.
b) Tính diện tích hình thang có độ dài hai đáy là 4cm và 6cm, đường cao 3cm
c) Tính diện tích hình bình hành có độ dài đáy là 8cm và đường cao ứng với cạnh đáy đó là 7cm
Câu 2: Viết tỉ số của cặp đoạn thẳng có độ dài như sau:AB = 7cm và CD = 14cm
Câu 3: a) Cho D ABC ∽ D MNI. Biết
AˆA^
= 800;
NˆN^
= 300. Tính
CˆC^
b) Cho DABD DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho.
Câu 4: Cho tam giác ABC có AB = 4cm, BC = 6cm. Lấy M thuộc AB sao cho AM = 2cm. Lấy N thuộc AC sao cho AN = 3cm. Chứng minh MN // BC.
Câu 5: Cho tam giác ABC vuông tại A có AB = 12cm, AC = 15cm. Vẽ AM là tia phân giác của góc A (M thuộc BC). Biết BM = 8cm. Tính NC?
Câu 6 : Cho có AB = 3cm, AC = 4,5cm, BC = 6cm.
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh
.
Câu 7: a) Cho tam giác ABC có AB = 4cm, BC = 6cm. Lấy M thuộc AB sao cho AM = 2cm. Biết MN // BC. Tính MN?
b) Cho tam giác ABC có AB = 15cm, AC = 18cm. Trên AB lấy điểm M sao cho AM = 12cm, qua điểm M kẻ đoạn thẳng MN//BC. Tính độ dài đoạn thẳng AN?
Câu 8:Cho tam giác ABC có AB = 6cm, AC = 9cm. Trên cạnh AB lấy điểm M sao cho AM = 4cm. Kẻ MN song song với BC (NAC). Tính AN?
Câu 9 : H.thang ABCD(AB//CD) có AB = 6cm, CD = 24cm, BD = 12cm. Chứng minh: DABDDBDC.
Câu 10 : Cho nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng.
Câu 11: Cho có
và
có MN = 6cm; MP = 8cm;
NP = 12cm. Hai tam giác ABC và MNP có đồng dạng không? Vì sao?
Câu 12: Cho góc nhọn xAy, trên tia Ax đặt hai đoạn thẳng AM = 10cm và AB = 12cm. Trên tia Ay đặt hai đoạn thẳng AN = 8cm và AC = 15cm. BN cắt CM tại H
Chứng minh đồng dạng với
Chứng minh
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
Đúng 0
Bình luận (0)
1 tính diện tích của hình thoiABCD, biết độ dài các đường chéo là AC=3cm;BD=4cm
2 Tính diện tích hình thoi MNPQ,biết độ dài các đường chéo là MP=7cm; NQ=4cm
Bạn nào giải rõ ràng và đầy đủ mình tich cho
diện tích hình thoi ABCD là:
(3*4):2=6 (cm2)
diện tích hình thoi MNPQ là:
(7*4):2=14 (cm2)
Đúng 0
Bình luận (0)
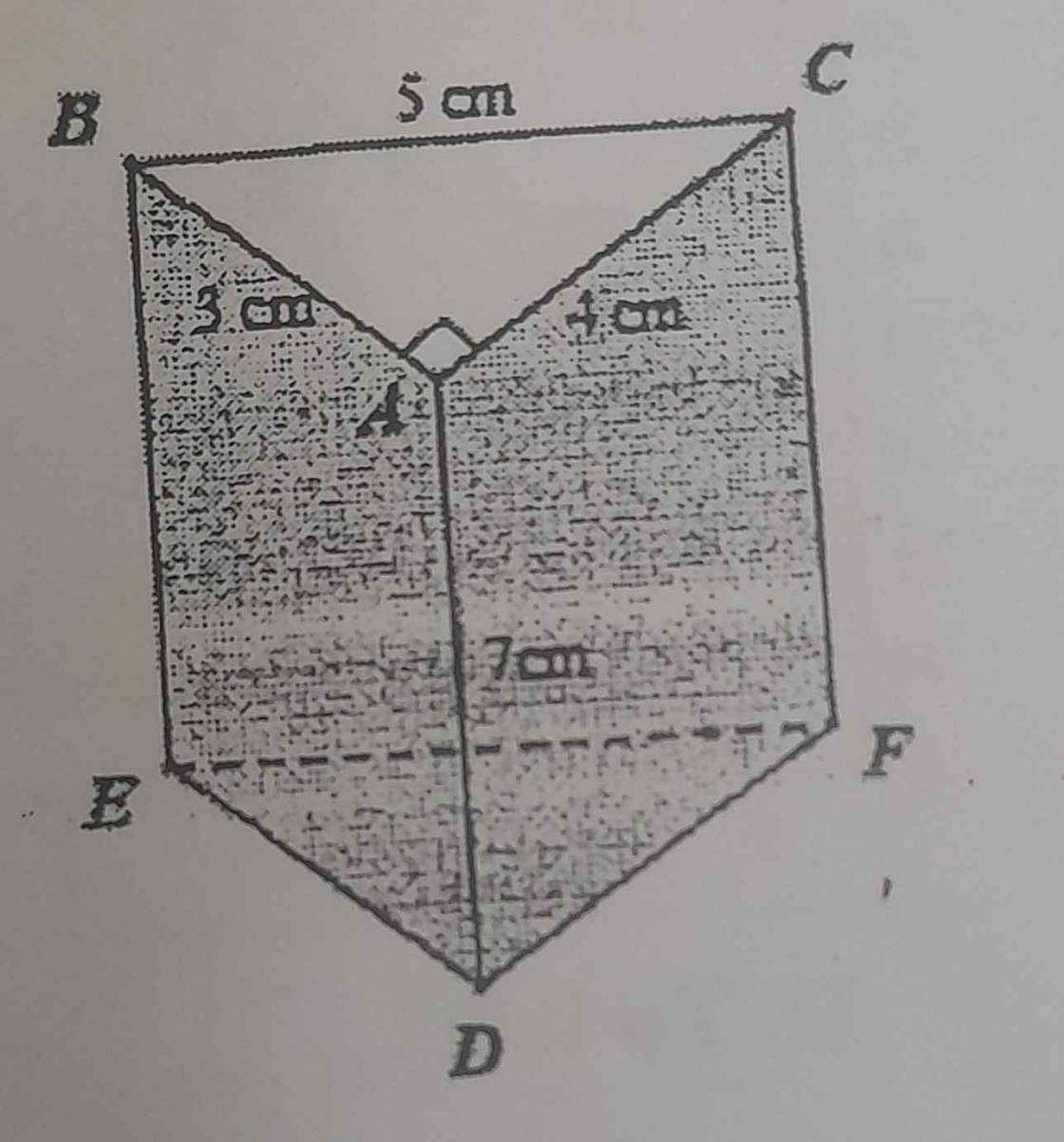
Cho hình lăng trụ đứng tam giác ABC.DEF, biết AB= 3cm; AC=4cm; BC = 5cm và AD =7cm (hình vẽ). Hãy tính diện tích xung quanh và thể tích của hình lăng trụ?
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh của hình trụ là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích của lăng trụ là:
\(V=S_{đáy}\cdot cao=6\cdot7=42\left(cm^3\right)\)
Đúng 2
Bình luận (0)
Cho ba điểm A, B, C thẳng hàng. Tìm điểm nằm giữa hai điểm còn lại trong các trường hợp sau:
a. AB = 5cm, BC = 2cm, AC = 7cm
b. AB = 4cm, BC = 7cm, AC = 3cm
a. Ta có AB + BC = AC ( vì 5 + 2 = 7)
Vậy điểm B nằm giữa hai điểm A, C
b. Ta có AB + AC = BC ( vì 4 + 3 = 7)
Vậy điểm A nằm giữa hai điểm B, C
Đúng 0
Bình luận (0)
Tính (theo mẫu):
a) 2cm + 3cm = 5cm b) 6cm - 2cm = 4cm
7cm + 1cm = 5cm - 3cm =
8cm + 2cm = 9cm - 4cm =
14cm + 5cm = 17cm - 7cm =
a) 2cm + 3cm = 5cm b) 6cm - 2cm = 4cm
7cm + 1cm = 8cm 5cm - 3cm = 2cm
8cm + 2cm = 10cm 9cm - 4cm = 5cm
14cm + 5cm = 19cm 17cm - 7cm = 10cm
Đúng 0
Bình luận (0)
P,Q,R, PQ = 7cm, QR = 4cm, PR = 3cm
a, 3 điểm P,Q,R có thẳng hàng không? Điểm nào nằm giữa hai điểm còn lại
b, E thuộc tia RP sao cho RE = 5cm, F thuộc tia RQ sao cho RF = 4cm. Tính PE, EF
a) Cho tam giác ABC = tam giác DEF. Biết A=27 độ, F =52 độ. Tính các góc còn lại của mỗi tam giác.
b) Cho tam giác ABC =tam giác MNP, biết AB +BC =7cm MN - NP = 3cm ,MP =4cm . Tính chu vi của mỗi tam giác.
Cho 3 điểm A,B,C thẳng hàng và AB = 4cm, AC = 3cm, BC = 7cm. Trong 3 điểm A,B,C điểm nào nằm giữa hai điểm còn lại .
Vì AB + BC = AC nên 3 điểm A ; B ; C thẳng hàng
Đúng 2
Bình luận (0)
cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm, 3,6cm; cạnh BC=4cm. tính diện tích tam giác ABC và tính hai cạnh còn lại của tam giác ABC
tính diện tích hcn biết nếu tăng chiều dài hcn đó thêm 7cm và giữ nguyên chiều rộng thì diện tích tăng thêm 119cm2 còn nếu giữ nguyên chiều dài và giảm chiều rộng đi 3cm thì diện tích giảm đi 84cm2