Xét các số phức z thỏa mãn z + 1 - i + z - 3 + i = 2 5 . Tìm giá trị nhỏ nhất của P = z + 2 + 4 i .
A. P m i n = 11 5 5
B. P m i n = 2 + 2
C. P m i n = 5
D. P m i n = 5 - 2
Xét các số phức z thỏa mãn z - 1 + i ( z + z ¯ ) i + 1 là số thực. Tập hợp các điểm biểu diễn các số phức z 2 là parabol có tọa độ đỉnh
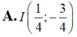
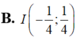
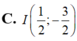

Xét các số phức z thỏa mãn z - 1 + i ( z + z ¯ ) i + 1 là số thực. Tập hợp các điểm biểu diễn của số phức w = z 2 là parabol có đỉnh
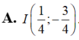
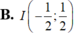
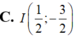
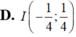
Xét các số phức z thỏa mãn z - 1 - 3 i . Số phức z mà z - 1 nhỏ nhất là:
A. z = 1 + 5 i
B. z = 1 + i
C. z = 1 + 3 i
D. z = 1 - i
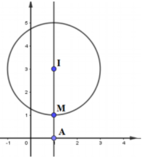
Tập hợp các điểm M biểu diễn của các số phức thỏa mãn z - 1 - 3 i = 2 là đường tròn:
![]()
z - 1 là khoảng cách từ điểm M đến điểm A(1,0). Khoảng cách này nhỏ nhất khi và chỉ khi M nằm giữa I và A (với I(1,3) là tâm đường tròn
![]()
Dễ dàng tính được M(1,1).
Vậy, số phức z thỏa mãn là z = 1 + i .
Chọn B.
Xét các số phức z thỏa mãn z - 1 + i z + z + i + 1 là số thực. Tập hợp các điểm biểu diễn của số phức w = z 2 là parabol có đỉnh
A. I 1 4 ; 3 4
B. I - 1 2 ; 1 2
C. I 1 2 ; 3 2
D. I - 1 4 ; 1 4
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Xét các số phức z thỏa mãn điều kiện z - 3 + 2 i = 5 Trong mặt phẳng tọa độ Oxr, tập hợp các điểm biểu diễn các số phức w = z + 1 -i là
A. Đường tròn tâm I(4;-3), bán kính R = 5.
B. Đường tròn tâm I(-4;3), bán kính R = 5.
C. Đường tròn tâm I(-2;1), bán kính R = 5.
D. Đường tròn tâm I(3;-2), bán kính R = 5.
Xét các số phức thỏa mãn : |z-2i| = |z-4+i| Tìm z m i n .
A. z m i n = 1 2
B. z m i n = 1
C. z m i n = 13 10
D. z m i n = 3 2