Cho hàm số y= 2 x 2 - 1 . Chọn phát biểu đúng.
![]()
![]()
![]()
![]()
Cho hàm số y = log 2 2 x 2 − x − 1 . Hãy chọn phát biểu đúng
A. Hàm số nghịch biến trên − ∞ ; − 1 2 đồng biến trên 1 ; + ∞
B. Hàm số đồng biến trên − ∞ ; − 1 2 và 1 ; + ∞
C. Hàm số nghịch biến trên − ∞ ; − 1 2 và 1 ; + ∞
D. Hàm số đồng biến trên nghịch biến − ∞ ; − 1 2 trên 1 ; + ∞
Đáp án A
Điều kiện để hàm số xác định là 2 x 2 − x − 1 > 0 ⇔ x > 1 x < − 1 2 *
Với điều kiện * ta có 4 x − 1 2 x 2 − x − 1 ln 2 > 0 ⇔ x ∈ 1 ; + ∞ , y ' < 0 ⇔ x ∈ − ∞ ; − 1 2 ⇒
Hàm số nghịch biến trên − ∞ ; − 1 2 , đồng biến trên 1 ; + ∞
Cho hàm số y = x 2 - x + 1 x - 1 . Chọn phát biểu đúng
![]()
![]()
![]()
![]()
Cho hàm số
y
=
x
-
1
x
2
-
x
-
6
Chọn phát biểu đúng trong các phát biểu sau:
A. Đồ thị hàm số có đúng một đường tiệm cận đứng và một đường tiệm cận ngang
B. Đồ thị hàm số có đúng hai đường tiệm cận đứng và hai đường tiệm cận ngang
C. Đồ thị hàm số có đúng một đường tiệm cận đứng và hai đường tiệm cận ngang
D. Đồ thị hàm số có đúng hai đường tiệm cận đứng và một đường tiệm cận ngang
Cho hàm số y = 1 x - 1 chọn phát biểu đúng trong các phát biểu sau
A. Đồ thị hàm số chỉ có tiệm cận đứng x = 1
B. Đồ thị hàm số chỉ có tiệm cận ngang y = 0
C. Đồ thị hàm số có tiệm cận đứng x = 1 và tiệm cận ngang y = 0
D. Đồ thị hàm số không có tiệm cận đứng
Đáp án C.
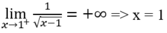 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
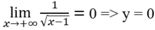 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.
Cho hàm số y = x 2 x - 1 . Chọn phát biểu đúng
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có bảng biến thiên như sau:
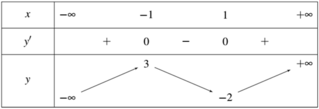
(I): Tập xác định của f(x): R \ {1}
(II): Hàm số f(x) có đúng 1 điểm cực trị
(III): min f(x) = -2
(IV): A(-1; 3) là điểm cực đại của đồ thị hàm số
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 2
B. 3
C. 1
D. 0
Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng
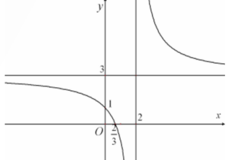
Cho các phát biểu sau (1): Hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị là (C) không có cực trị (2).Hàm số y = x 3 + 3 x 2 + 3 x + 1 có điểm uốn là U(-1;0) (3). Đồ thị hàm số y = 3 x - 2 x - 2 có dạng.Hàm số y = 2 x + 1 x + 1 có lim x → 1 + 2 x + 1 x + 1 = - ∞ và lim x → 1 - 2 x + 1 x + 1 = + ∞ .Số các phát biểu đúng là:
A. 1
B. 2
C. 3
D. 0
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
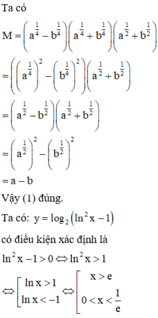
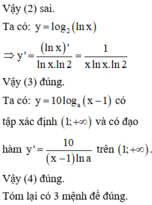
Cho hàm số y = log 2 x . Xét các phát biểu
(1) Hàm số y = log 2 x đồng biến trên khoảng (0;+∞) .
(2) Hàm số y = log 2 x có một điểm cực tiểu.
(3) Đồ thị hàm số y = log 2 x có tiệm cận.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Đáp án D
Phương pháp:
Đánh giá từng đáp án.
Cách giải:
(1) Hàm số y = log2x đồng biến trên khoảng (0;+∞): đúng, do 2 > 1
(2) Hàm số y = log2x có một điểm cực tiểu: sai, hàm số y = log2x luôn đồng biến trên (0;+∞)
(3) Đồ thị hàm số y = log2x có tiệm cận: đúng, tiệm cận đó là đường x = 0
Số phát biểu đúng là 2.