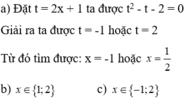Giải phương trình (5x2 - 2x + 10)2= (3x2 + 10x - 8)2

Những câu hỏi liên quan
Giải các phương trình sau: ( 5 x 2 - 2 x + 10 ) 2 = ( 3 x 2 + 10 x - 8 ) 2

![]()
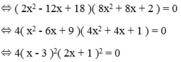
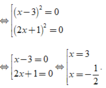
Vậy phương trình đã cho có tập nghiệm S = {- 1/2; 3}.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
3
x
+
1
−
2
x
+
2
4
x
+
5
x
2
+
3
x
+
2...
Đọc tiếp
Giải các phương trình sau:
a) 3 x + 1 − 2 x + 2 = 4 x + 5 x 2 + 3 x + 2 ;
b) 2 x 2 + x + 6 x 3 − 8 + 2 2 − x = 3 x 2 + 2 x + 4 .
Tập nghiệm của phương trình
5
x
2
–
2
x
+
10
2
3
x
2
+...
Đọc tiếp
Tập nghiệm của phương trình 5 x 2 – 2 x + 10 2 = 3 x 2 + 10 x - 8 2 là
A. S = { 1 2 ; 3}
B. S = { 1 2 ; -3}
C. S = {- 1 2 ; 3}
D. S = {- 1 2 ; -3}
Ta có:
5 x 2 − 2 x + 10 2 = 3 x 2 + 10 x − 8 2 ⇔ 5 x 2 − 2 x + 10 2 − 3 x 2 + 10 x − 8 2 = 0 ⇔ 5 x 2 − 2 x + 10 + 3 x 2 + 10 x − 8 5 x 2 − 2 x + 10 − 3 x 2 − 10 x + 8 = 0 ⇔ 8 x 2 + 8 x + 2 2 x 2 − 12 x + 18 = 0 ⇔ 2 4 x 2 + 4 x + 1 .2 x 2 − 6 x + 9 = 0 ⇔ 2 x + 1 2 x − 3 2 = 0 ⇔ 2 x + 1 2 = 0 x − 3 2 = 0 ⇔ 2 x + 1 = 0 x − 3 = 0 ⇔ x = − 1 2 x = 3
Vậy tập nghiệm của phương trình là S = − 1 2 ; 3
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Giải phương trình
a) \((x^2-1)(x+2)(x-3)=(x-1)(x^2-4)(x+5)\)
b) \( (5x2 - 2x + 10)^2 = (x^2 + 10x - 8)^2\)
\(a,\left(x^2-1\right)\left(x+2\right)\left(x-3\right)=\left(x-1\right)\left(x^2-4\right)\left(x+5\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x+1\right)\left(x-3\right)-\left(x-1\right)\left(x+2\right)\left(x-2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(7-5x\right)=0\)
\(\Leftrightarrow x-1=0;x+2=0\)hoặc \(7-5x=0\)
\(\Leftrightarrow x=1;x=-2\)hoặc \(x=\frac{7}{5}\)
KL....
\(b,\left(5x^2-2x+10\right)^2=\left(x^2+10x-8\right)^2\)
\(\Leftrightarrow\left(5x^2-2x+10\right)^2-\left(x^2+10x-8\right)^2=0\)
\(\Leftrightarrow\left(5x^2-2x+10-x^2-10x+8\right)\left(5x^2-2x+10+x^2+10x-8\right)=0\)
\(\Leftrightarrow\left(4x^2-12x+18\right)\left(6x^2+8x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+\frac{9}{2}\right)\left(6x^2+6x+2x+2\right)=0\)
\(\Leftrightarrow\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}+\frac{9}{4}\right)\left(6x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[\left(x-\frac{3}{2}\right)^2+\frac{9}{4}\right]\left(3x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\x+1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{1}{3}\\x=-1\end{cases}}\)Vì \(\left(x-\frac{3}{2}\right)^2+\frac{9}{4}>0\forall x\)
Vậy ..
Giải các phương trình sau:a)
2
x
+
1
2
−
2
x
−
1
2
;
b)
x
2
−
3
x
2
+
5
x...
Đọc tiếp
Giải các phương trình sau:
a) 2 x + 1 2 − 2 x − 1 = 2 ;
b) x 2 − 3 x 2 + 5 x 2 − 3 x + 6 = 0 ;
c) x 2 − x − 1 x 2 − x − 2 = 0 .
giải phương trình sau;
(5x^2-2x+10)^2=(3x^2+10x-8)^2
TH1: 5x2 - 2x + 10 = 3x2 + 10x - 8
=> 2x2 - 12x + 18 = 0
=> x2 - 6x + 9 = 0
=> (x - 3)2 = 0
=> x = 3
TH2: 5x2 - 2x + 10 = - 3x2 - 10x + 8
=> 8x2 + 8x + 2 = 0
=> 4x2 + 4x + 1 = 0
=> (2x + 1)2 = 0
=> x = -1/2
Vậy x = 3 , x = -1/2
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương:
a
)
x
4
−
5
x
2
+
4
0
b
)
2
x
4
−
3...
Đọc tiếp
Giải các phương trình trùng phương:
a ) x 4 − 5 x 2 + 4 = 0 b ) 2 x 4 − 3 x 2 − 2 = 0 c ) 3 x 4 + 10 x 2 + 3 = 0
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
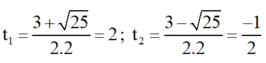
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
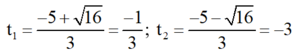
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình và hệ phương trình sau:
a
,
5
x
2
−
16
x
+
3
0
b
,
x
4
+
9
x
2
−
10
0
c
,
3
x
−...
Đọc tiếp
Giải các phương trình và hệ phương trình sau:
a , 5 x 2 − 16 x + 3 = 0 b , x 4 + 9 x 2 − 10 = 0 c , 3 x − 2 y = 10 x + 3 y = 7
a) Ta có: Δ = 196 > 0
Phương trình có 2 nghiệm x 1 = 3 , x 2 = 1 5
b) Đặt t = x 2 , t ≥ 0 , phương trình trở thành t 2 + 9 t − 10 = 0
Giải ra được t=1 (nhận); t= -10 (loại)
Khi t=1, ta có x 2 = 1 ⇔ x = ± 1 .
c) 3 x − 2 y = 10 x + 3 y = 7 ⇔ 3 x − 2 y = 10 ( 1 ) 3 x + 9 y = 21 ( 2 )
(1) – (2) từng vế ta được: y=1
Thay y= 1 vào (1) ta được x= 4
Vậy hệ phương trình có nghiệm duy nhất là x= 4; y= 1.
Đúng 0
Bình luận (0)
Giải các phương trình tích sau:1.a)(3x – 2)(4x + 5) 0 b) (2,3x – 6,9)(0,1x + 2) 0c)(4x + 2)(x2 + 1) 0 d) (2x + 7)(x – 5)(5x + 1) 02. a)(3x + 2)(x2 – 1) (9x2 – 4)(x + 1) b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) 0c)2x(x – 3) + 5(x – 3) 0 d)(3x – 1)(x2 + 2) (3x – 1)(7x – 10)3.a)(2x – 5)2 – (x + 2)2 0 b)(3x2 + 10x – 8)2 (5x2 – 2x + 10)2c)(x2 – 2x + 1) – 4 0 d)4x2 + 4x + 1 x24. a) 3x2 + 2x – 1 0 b) x2 – 5x + 6 0c) x2 – 3x + 2 0 d) 2x2 – 6x + 1 0 ...
Đọc tiếp
Giải các phương trình tích sau:
1.a)(3x – 2)(4x + 5) = 0 b) (2,3x – 6,9)(0,1x + 2) = 0
c)(4x + 2)(x2 + 1) = 0 d) (2x + 7)(x – 5)(5x + 1) = 0
2. a)(3x + 2)(x2 – 1) = (9x2 – 4)(x + 1)
b)x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) = 0
c)2x(x – 3) + 5(x – 3) = 0 d)(3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
3.a)(2x – 5)2 – (x + 2)2 = 0 b)(3x2 + 10x – 8)2 = (5x2 – 2x + 10)2
c)(x2 – 2x + 1) – 4 = 0 d)4x2 + 4x + 1 = x2
4. a) 3x2 + 2x – 1 = 0 b) x2 – 5x + 6 = 0
c) x2 – 3x + 2 = 0 d) 2x2 – 6x + 1 = 0
e) 4x2 – 12x + 5 = 0 f) 2x2 + 5x + 3 = 0
Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5
bài 2:
a, (3x+2)(x^2-1)=(9x^2-4)(x+1)
(3x+2)(x-1)(x+1)=(3x-2)(3x+2)(x+1)
(3x+2)(x-1)(x+1)-(3x-2)(3x+2)(x+1)=0
(3x+2)(x+1)(1-2x)=0
b, x(x+3)(x-3)-(x-2)(x^2-2x+4)=0
x(x^2-9)-(x^3+8)=0
x^3-9x-x^3-8=0
-9x-8=0
tự tìm x nha
Đúng 0
Bình luận (0)
Giải bất phương trình sau:a) 3x2 - 10x - 8 0b) x2 + (x + 2)(11 - 7x) 12c) 3x - 4/x + 2 ≥ 4d) x2 - x/1 + x2 ≤ 1e) x/1 - 2x x2 - x - 1/1 - 4x2Giúp mik vs mọi người ơi mai mik ktra rồi THANKS TRƯỚC NHA!
Đọc tiếp
Giải bất phương trình sau:
a) 3x2 - 10x - 8 > 0
b) x2 + (x + 2)(11 - 7x) > 12
c) 3x - 4/x + 2 ≥ 4
d) x2 - x/1 + x2 ≤ 1
e) x/1 - 2x > x2 - x - 1/1 - 4x2
Giúp mik vs mọi người ơi mai mik ktra rồi THANKS TRƯỚC NHA!