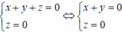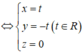Trong không gian với hệ tọa độ Oxy, cho đường thẳng ∆ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxy, cho đường thẳng ∆ : x 2 = y - 3 - 1 = z + 2 3 cắt mặt phẳng (P): x-2y+z+1=0 tại điểm M. Khi đó tọa độ điểm M là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Trong không gian với hệ tọa độ Oxy, cho đường thẳng d : x − 1 1 = y − 2 = z − 1 2 . Điểm nào dưới đây KHÔNG thuộc d?
A. E 2 ; − 2 ; 3
B. N 1 ; 0 ; 1
C. F 3 ; − 4 ; 5
D. M 0 ; 2 ; 1
Trong không gian với hệ tọa độ Oxy, cho đường thẳng △ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất
A. M(5;2;-4)
B. M(-1;-1;-1)
C. M(1;0;-2)
D. M(3;1;-3)
Trong không gian với hệ tọa độ Oxy, cho hai đường thẳng d 1 : x = 2 + t y = 1 − t z = 2 t và d 2 : x = 2 − 2 t y = 3 z = t . Khoảng cách từ điểm M − 2 ; 4 ; − 1 đến mặt phẳng cách đều hai đường thẳng d 1 và d 2 là:
A. 15 15
B. 2 15 15
C. 30 15
D. 2 30 15
Đáp án D
Nhận thấy d 1 ⊥ d 2 . Gọi α là mặt phẳng cách đều d 1 và d 2 nên cả hai đường thẳng đều song song với mặt phẳng α . Khi đó, vector pháp tuyến a → của mặt phẳng α cùng phương với vector u 1 → , u 2 → (với u 1 → , u 2 → lần lượt là các vec tơ chỉ phương của hai đường thẳng d 1 , d 2 ).
+ Chọn a → = 1 ; 5 ; 2 , suy ra phương trình mặt phẳng α có dạng
α : x + 5 y + 2 z + d = 0
Chọn A 2 ; 1 ; 0 và B 2 ; 3 ; 0 lần lượt thuộc đường thẳng d 1 và d 2 , ta có
d A ; α = d B ; β ⇒ d = − 12 ⇒ α : x + 5 y + 2 z − 12 = 0
+ Khoảng cách từ điểm M − 2 ; 4 ; − 1 đến mặt phẳng α : d M ; α = 2 30 15
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x = 1 + 2 t y = t z = 2 - t . Gọi d’là hình chiếu vuông góc của đường thẳng d trên mặt phẳng (Oxy). Đường thẳng d’ có một véc tơ chỉ phương là
A. u 1 → = ( 2 ; 0 ; 1 )
B. u 1 → = ( 1 ; 1 ; 0 )
C. u 1 → = ( - 2 ; 1 ; 0 )
D. u 1 → = ( 2 ; 1 ; 0 )
Đáp án D
Gọi M(1+2t;2t;2-t) là giao điểm của d và (Oxy): z =0
![]()
Gọi N(1;0;2) là điểm thuộc d. Hình chiếu của N lên (Oxy) là I(1;0;0)
![]()
là một véc tơ chỉ phương của d’
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3 2 = y + 2 - 1 = z + 1 4 . Điểm nào sau đây không thuộc đường thẳng
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ , cho bốn đường thẳng:
d 1 : x - 3 1 = y + 1 - 2 = z + 1 1 ; d 2 : x 1 = y - 2 = z - 1 1
d 3 : x - 1 2 = y + 1 1 = z - 1 1 ; d 4 : x 1 = y - 1 - 1 = z - 1
Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0
B. 2
C. Vô số.
D. 1
Chọn A
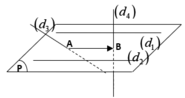
Ta có d1 song song d2, phương trình mặt phẳng chứa hai đường thẳng d1, d2 là
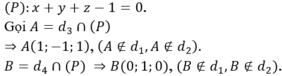
Mà ![]() cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + y + z = 0 . Gọi d là giao tuyến của (P) với mặt phẳng (Oxy). Viết phương trình đường thẳng d
A. x = 0 y = t z = - t
B. x = t y = - t z = 0
C. x = t y = t z = - 2 t
D. x = t y = 0 z = - t
Chọn đáp án B
Phương trình đường thẳng d là giao tuyến của hai mặt phẳng (P) và (Oxy) thỏa mãn hệ phương trình: