Trong không gian Oxyz, cho ba vectơ a → = ( 2 ; - 5 ; 3 ) , b → = ( 0 ; 2 ; - 1 ) , c → = 1 ; 7 ; 2 . Tọa độ vectơ x → = 4 a → - 1 3 b → + 3 c → là:
![]()
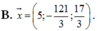
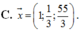
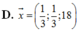
Trong không gian Oxyz, cho ba vectơ a → = 2 ; - 5 ; 3 , b → = 0 ; 2 ; - 1 , c → = 1 ; 7 ; 2 . Tọa độ vectơ x → = 4 a → - 1 3 b → + 3 c → là:
A. x → = 11 ; 5 3 ; 53 3
B. x → = 5 ; - 121 3 ; 17 3 .
C. x → = 11 ; 1 3 ; 55 3
D. x → = 1 3 ; 1 3 ; 18
Trong không gian Oxyz, cho ba vectơ a → = 4 ; 3 ; − 2 , b → = 6 ; 5 ; 1 , c → = x ; 2 x ; 3 x + 2 . Để ba vectơ a → , b → , c → đồng phẳng thì giá trị của x là:
A. − 4 13
B. 13 4
C. 4 13
D. − 13 4
Đáp án C
Em có: a → , b → = 13 ; − 16 ; 2
Ba vectơ a → , b → , c → đồng phẳng thì a → , b → . c → = 0

Trong không gian Oxyz, cho ba vectơ ![]()
Tọa độ của vectơ ![]()
A. (4;3;9)
B. (4;3;21)
C. (2;-1;10)
D. (4;-1;10)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0); B(0;1;0); C(0;0-2). Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?
A. n ⇀ = ( 2 ; 2 ; - 1 )
B. n ⇀ = ( 1 ; 1 ; - 2 )
C. n ⇀ = ( - 2 ; 2 ; 1 )
D. n ⇀ = ( 2 ; - 2 ; - 1 )
Mặt phẳng (ABC) cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A(1;0;;0), B(0;1;0),C(0;0-2)
⇒ ( A B C ) : x 1 + y 1 + z - 2 = 1 ⇔ 2 x + 2 y - z + 2 = 0
⇒ ( A B C ) nhận vectơ n ⇀ = ( 2 ; 2 ; - 1 ) làm VTPT.
Chọn đáp án A.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A 1 ; 0 ; 0 , B 0 ; 1 ; 0 , C 0 ; 0 ; - 2 . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?
A. n → = 2 ; 2 ; - 1
B. n → = 1 ; 1 ; - 2
C. n → = - 2 ; 2 ; 1
D. n → = 2 ; - 2 ; - 1
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ a → = 2 ; 3 ; − 5 ; b → = 0 ; − 3 ; 4 ; c → = 1 ; − 2 ; 3 . Tọa độ vectơ n → = 3 a → + 2 b → − c → là:
A. n → = 5 ; 1 ; − 10
B. n → = 7 ; 1 ; − 4
C. n → = 5 ; 5 ; − 10
D. n → = 5 ; − 5 ; − 10
Đáp án C
n → = 3 2 ; 3 ; − 5 + 2 0 ; − 3 ; 4 − 1 ; − 2 ; 3 = 5 ; 5 ; − 10
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ u → = 1 ; 1 ; 2 , a → = 3 ; - 1 ; - 2 và v → = - 1 ; m ; m - 2 . Để vectơ u → , v → vuông góc với a → thì giá trị m bằng bao nhiêu?
A. m = 2
B. m = -2
C. m = 1
D. m = -1
Trong không gian Oxyz, cho ba vectơ ![]()
Trong các khẳng định sau, khẳng định nào đúng?
A. a → . b → c → = c → . b → a → với mọi a → , b → , c →
B. b → + a → c → = a → . c → + b → . c →
C. b → . c → a → ≥ 0
D. a → + b → + c → 2 < 0
Trong không gian Oxyz, cho ba vectơ ![]()
Trong các khẳng định sau, khẳng định nào đúng?
A. a → . b → . c → = b → . c → . a → với mọi a → , b → , c →
B. a → . b → . c → = b → . c → . a → ⇔ b → = 0 →
C. a → . b → . c → = b → . c → . a → ⇔ a → / / c →
D. a → . b → . c → ≤ a → . b → . c →