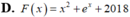Cho hàm số f(x) thỏa mãn f'(x) + 2x f(x) = 2 xe - x 2 và f(0)=1. Tất cả các nguyên hàm của x f x e x 2 là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
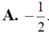
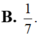
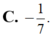
![]()
Cho hàm số f(x) thỏa mãn f ( 2 ) = - 2 9 và f ' ( x ) = 2 x [ f ( x ) ] 2 với mọi giá trị x thuộc R Giá trị của f(1) bằng
A. - 35 36
B. - 2 3
C. - 19 36
D. - 2 15
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho F(x) là một nguyên hàm của hàm số f ( x ) = e x + 2 x thỏa mãn F(0)=3/2. Tìm F(x)
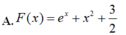
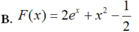
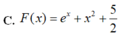
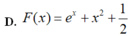
Cho hàm số f(x) thỏa mãn ∫ 1 2 ( 2 x + 3 ) . f ' ( x ) d x = 15 và 7 . f ( 2 ) - 5 . f ( 1 ) = 8 Tính I= ∫ 1 2 f ( x ) d x .
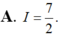
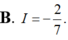

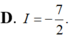
Cho hàm số y = f ( x ) thỏa mãn: f ( 2 x - 1 x + 2 ) = 3 x + 5 2 x - 1 ( x ≠ 2 ; 1 2 ) . Tìm lim x → + ∞ f ( x )
A. 4 3
B. 1 5
C. 3 2
D. 2 3
Cho hàm số y=f(x) xác định, có đạo hàm trên R thỏa mãn f 2 ( - x ) = ( x 2 + 2 x + 4 ) f ( x + 2 ) và f ( x ) ≠ 0 , ∀ x ∈ R . Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=2 là
A. y=-2x+4.
B. y=2x+4.
C. y=2x.
D. y=4x+4.
Xét hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn điều kiện f(1)=1 và f(2)=4.
Tính J = ∫ 1 2 f ' ( x ) + 2 x - f ( x ) + 1 x 2 d x
A. J = 1 + ln 4
B. J = 4 - ln 2
C. J = ln 2 - 1 2
D. J = 1 2 + ln 4
Cho hàm số y=f(x) liên tục trên R thỏa mãn f(2)=16 và ∫ 0 1 f ( 2 x ) d x = 2 Tích phân I = ∫ 0 2 x f ' ( x ) d x bằng
A. I=30
B. I=28
C. I=36
D. I=16
Cho hàm số f ( x ) = 2 x + e x . Tìm một nguyên hàm F(x) của hàm số f(x) thỏa mãn F(0)=2019
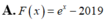
![]()
![]()