Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn f ' ( x ) 2 + f x f ' ' x ≥ 1 ∀ m ∈ 0 ; 1 và f 2 0 + f 0 . f ' 0 = 3 2 Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 x d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Những câu hỏi liên quan
Cho hàm số f(x) có đạo hàm cấp hai f(x) liên tục trên đoạn [0;1] thoả mãn f(1) f(0) 1; f(0) 2018 Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên đoạn [0;1] thoả mãn f(1) = f(0) = 1; f'(0) = 2018 Mệnh đề nào dưới đây đúng?
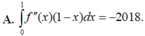
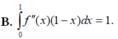
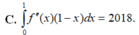
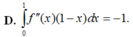
Cho hàm số f(x) có đạo hàm cấp hai f”(x) liên tục trên đoạn [0;1] thỏa mãn f(1) f(0) 1;f’(0) 2018 Mệnh đề nào dưới đây đúng? A.
∫
0
1
f
x
1
-
x
d
x
-
2018
B.
∫
0
1
f...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f”(x) liên tục trên đoạn [0;1] thỏa mãn f(1) = f(0) = 1;f’(0) = 2018 Mệnh đề nào dưới đây đúng?
A. ∫ 0 1 f " x 1 - x d x = - 2018
B. ∫ 0 1 f " x 1 - x d x = - 1
C. ∫ 0 1 f " x 1 - x d x = 2018
D. ∫ 0 1 f " x 1 - x d x = 1
Cho hàm số f(x) có đạo hàm cấp hai f″(x) liên tục trên đoạn [0;1] thoả mãn f(1)f(0)1,f(0)2018. Mệnh đề nào dưới đây đúng ? A.
∫
0
1
f
(
x
)
(
1
-
x
)
d
x
-2018 B.
∫
0
1
f
(
x
)
(
1
-
x
)...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f″(x) liên tục trên đoạn [0;1] thoả mãn f(1)=f(0)=1,f'(0)=2018. Mệnh đề nào dưới đây đúng ?
A. ∫ 0 1 f ' ' ( x ) ( 1 - x ) d x = -2018
B. ∫ 0 1 f ' ' ( x ) ( 1 - x ) d x = 1
C. ∫ 0 1 f ' ' ( x ) ( 1 - x ) d x = 2018
D. ∫ 0 1 f ' ' ( x ) ( 1 - x ) d x = -1
Cho hàm số
f
x
có đạo hàm cấp hai
f
x
liên tục trên đoạn [0;1] thoả mãn
f
1
f
(
0
)
1
,
f
(
0
)
2018
Mệnh đề nào dưới đây đúng ? A.
∫
0...
Đọc tiếp
Cho hàm số f x có đạo hàm cấp hai f ' ' x liên tục trên đoạn [0;1] thoả mãn f 1 = f ( 0 ) = 1 , f ' ( 0 ) = 2018 Mệnh đề nào dưới đây đúng ?
A. ∫ 0 1 f ' ' ( x ) 1 - x d x = - 2018 .
B. ∫ 0 1 f ' ' ( x ) 1 - x d x = 1 .
C. ∫ 0 1 f ' ' ( x ) 1 - x d x = 2018 .
D. ∫ 0 1 f ' ' ( x ) 1 - x d x = - 1 .
Cho hàm số y f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn
∫
0
1
e
x
f
(
x
)
d
x
∫
0
1
e
x
f
(
x
)
d
x
∫
0
1...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn ∫ 0 1 e x f ( x ) d x = ∫ 0 1 e x f ' ( x ) d x = ∫ 0 1 e x f ' ' ( x ) d x ≠ 0 . Giá trị của biểu thức e f ' ( 1 ) - f ' ( 0 ) e f ( 1 ) - f ( 0 ) bằng
A. -2.
B. -1.
C. 2.
D. 1.
Cho hàm số yf(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x
f
x
d
x
∫
0
1
e...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn ∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x ≠ 0 . Giá trị của biểu thức e . f ' 1 − f ' 0 e . f 1 − f 0 bằng
A.-2
B.-1
C.2
D.1
Đáp án D
∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x = k ≠ 0
Đặt
u = e x d v = f ' x d x ⇒ d u = e x d x v = f x ⇒ ∫ 0 1 e x f ' x d x = e x f x 0 1 − ∫ 0 1 e x f x d x
⇒ k = e . f 1 − f 0 − k ⇒ e f 1 − f 0 = 2 k .
Đặt
u = e x d v = f ' ' x d x ⇒ d u = e x d x v = f ' x ⇒ ∫ 0 1 e x f ' ' x d x = e x f ' x 0 1 − ∫ 0 1 e x f ' x d x
⇒ k = e . f ' 1 − f ' 0 − k ⇒ e . f ' 1 − f ' 0 = 2 k .
Vậy e . f ' 1 − f ' 0 e . f 1 − f 0 = 2 k 2 k = 1
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn ∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x ≠ 0 . Giá trị của biểu thức e . f ' 1 − f ' 0 e . f 1 − f 0 bằng
A. -2
B. -1
C. 2
D. 1
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn
[
f
(
x
)
]
2
+
f
(
x
)
f
(
x
)
≥
1
,
∀
x
∈
[
0
;
1
]
và
f
2
(
0
)
+
f
(...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn [ f ' ( x ) ] 2 + f ( x ) f '' ( x ) ≥ 1 , ∀ x ∈ [ 0 ; 1 ] và f 2 ( 0 ) + f ( 0 ) . f ' ( 0 ) = 3 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 ( x ) d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Cho hàm số
y
f
x
có đạo hàm cấp hai liên tục trên đoạn
0
;
1
thoả mãn
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x
f
x
d
x
∫...
Đọc tiếp
Cho hàm số y = f x có đạo hàm cấp hai liên tục trên đoạn 0 ; 1 thoả mãn ∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x ≠ 0 . Giá trị của biểu thức e f ' ( 1 ) - f ' ( 0 ) e f ( 1 ) - f ( 0 ) bằng
A. - 2 .
B. - 1
C. 2.
D. 1.
