Đáp án B

Giả sử đáy của hình chóp có n cạnh => 2n = 20 <=> n = 10 => số mặt là 10 + 1 = 11.

Đáp án B

Giả sử đáy của hình chóp có n cạnh ⇒ 2 n = 20 ⇔ n = 10 ⇒  số mặt là  10 + 1 = 11

Chọn B

Số cạnh bên của hình chóp bằng số cạnh đáy.

Suy ra số cạnh bên của hình chóp là:  20 2 = 10   cạnh.

Vậy hình chóp có 10 mặt bên và 1 mặt đáy.

Chọn D.

Gọi số mặt của hình chóp là n n ∈ N *  

=> số mặt bên của hình chóp là n-1 . Suy ra số cạnh của đa giác đáy hình chóp có n-1 cạnh.

Vậy số cạnh bên của hình chóp là 20-(n-1)=21-n

Mặt khác số cạnh bên của hình chóp bằng số mặt bên của hình chóp nên ta có:

=> n-1=21-n => n=11

Chọn đáp án B

Số cạnh bên của hình chóp bằng số cạnh đáy

Suy ra số cạnh bên của hình chóp là:  20 2 = 10 cạnh

Vậy hình chóp có 10 mặt bên và 1 mặt đáy

Đáp án là C

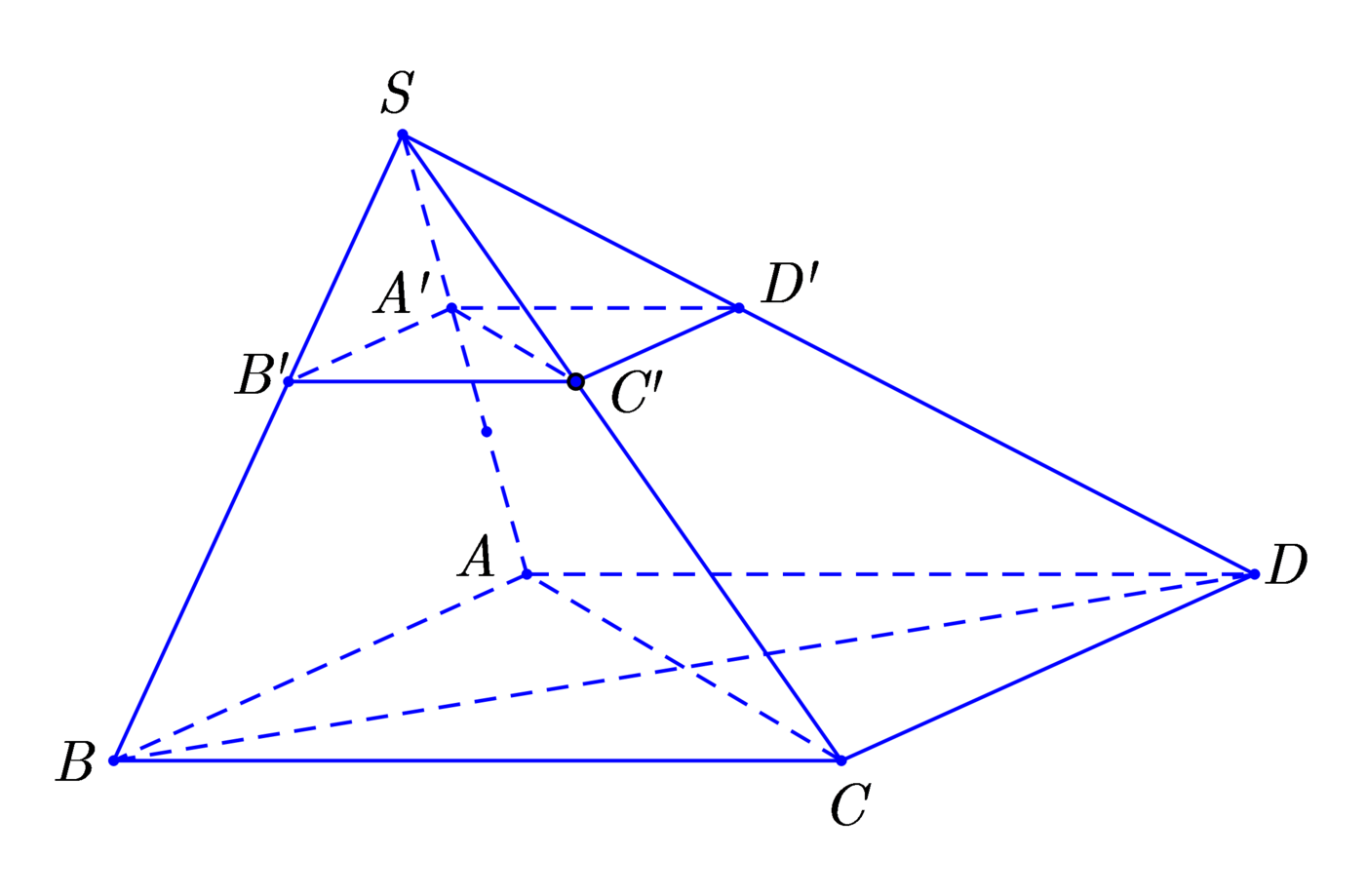
V S . A ' B ' C ' V S . A B C = 1 27 ⇒ V S . A ' B ' C ' = 1 27 V S . A B C ⇒ V S . A B C D = 2 V S . A ' B ' C ' = 2 27 . 1 2 V S . A B C D = V 27 .

Chọn A.

Chóp n- giác bao gồm n cạnh bên và đáy là n-giác Þ Có tất cả 2n cạnh.

Theo bài ra ta có: 2n = 10 Û n = 5. Suy ra hình chóp có 10 cạnh là chóp ngũ giác, có 5 mặt bên và 1 mặt đáy

Đáp án A.

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)

Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)

\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên  và đáy hay \(\widehat{SMO}=60^0\)

\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)

\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)