Có tất cả bao nhiêu giá trị nguyên của m ≥ - 10 sao cho đồ thị hàm số y = x 2 + x - 1 x 2 + ( m - 1 ) x + 1 có đúng một tiệm cận đứng?
A. 11.
B. 10.
C. 12.
D. 9.
Có tất cả bao nhiêu giá trị nguyên của m
≥
10
sao cho đồ thị hàm số  có đúng một tiệm cận đứng?
có đúng một tiệm cận đứng?
A. 11
B. 10
C. 12
D. 9
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên
A. 1.
B. 2.
C. 3.
D. 4.
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên?
A. 1
B. 2
C. 3
D. 4
Hỏi có tất cả bao nhiêu giá trị nguyên của m để đồ thị hàm số y = 2 x 3 - 3 ( m + 3 ) x 2 + 18 m x - 8 tiếp xúc với trục hoành?
A. 1
B. 2
C. 3
D. 0
Cho hàm số y = 12 + 4 x - x 2 x 2 - 6 x + 2 m có đồ thị ( C) . Gọi tập S tất cả các giá trị của tham số thực m để ( C) có đúng hai tiệm cận đứng. Hỏi tập S có bao nhiêu giá trị nguyên
A. 0
B. 1
C. 3
D. 4
ĐKXĐ: 0 ≤ x ≤ 4 x 2 - 6 x + 2 m > 0
Ta có
12
+
4
x
-
x
2
≠
0
∀
x
nên để ( C) có hai tiệm cận đứng thì phương trình
x
2
-
6
x
+
2
m
=
0
⇔
x
2
-
6
x
+
2
m
=
0
(
*
)
có hai nghiệm phân biệt thuộc [ 0; 4]
Đế phương trình có 2 nghiệm phân biệt thì ∆ ' = 9 - 2 m > 0 ⇔ m < 9 2
Gọi 2 nghiệm phân biệt của (*) là x1< x2 ta có 0≤ x1< x2≤ 4.
Theo định lí Vi-et ta có x 1 + x 2 = 6 x 1 x 2 = 2 m
Khi đó

Kết hợp nghiệm ta có 4 ≤ m ≤ 9 2
Mà m nguyên nên m= 4
Chọn B.
Cho hàm số y= x4- (2m-1) x2+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là
A. 1
B. 2
C. 3
D. 4
+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
=x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2= 1 hoặc x2= 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
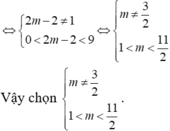
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.
Chọn D.
Cho hàm số y = f x = x 4 - 2 m 2 + 6 - 2 m có đồ thị C m với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m để cắt trục hoành tại 4 điểm phân biệt?
A. 1
B. 3
C. 4
D. 2
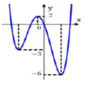
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
A. 9
B. 7
C. 12
D. 18
Cho hàm số y = x + 2 x có đồ thị là (C) và đường thẳng d : y = x + m . Có tất cả bao nhiêu giá trị nguyên của tham số m trên đoạn 0 ; 2018 để đường thẳng (d) cắt (C) tại hai điểm phân biệt A;B sao cho tam giác MAB cân tại M, với M 1 2 ; 1 2 .
A. 2016
B. 2017
C. 2019
D. 2018
Đáp án D
Phương trình hoành độ giao điểm của )C) và(d) là
x + 2 x = x + m ⇔ x ≠ 0 x 2 + m − 1 x − 2 = 0 *
Để (C) cắt (d) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân biệt khác 0 ⇔ m ∈ ℝ
Khi đó, gọi A x 1 ; x 1 + 1 ; B x 2 ; x 2 + m ⇒ x 1 + x 2 = 1 − m là tọa độ giao điểm của (C) và(d)
Ta có: A B → = x 2 − x 1 ; x 2 − x 1 ⇒ u A B → = 1 ; 1 ; trung điểm AB là: I 1 − m 2 ; 1 + m 2
m = 0 ⇒ M , A , B thẳng hang (loại m = 0 )
Phương trình trung trực là: x + y − 1 = 0
Do M ∈ d ⇒ Δ M A D luôn cân tại M
Kết hợp với m ∈ ℤ và có 2018 giá trị m cần tìm