Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.

mình trình bày hơi dài mong bạn thông cảm   

Làm giúp em đi ạ😗

Đáp án B

Đáp án B.

Phương pháp: 

Bất phương trình m ≥ f x ,    x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .  

Cách giải:

ĐKXĐ:  0 < x < 1

3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x

⇔ m ≥ x x + 1 − x 1 − x x − x 2 ,    x ∈ 0 ; 1

Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2  

Xét

f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1  

Đặt t = x + 1 − x ,    t ∈ 1 ; 2  

Khi đó,  

f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t

g ' t = − t 4 − 3 t 2 − 1 2 < 0 ,     ∀ t ∈ 1 ; 2  

⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2  

Mà

m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒

Có 7 giá trị thỏa mãn.

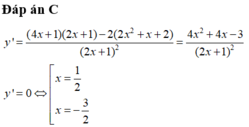
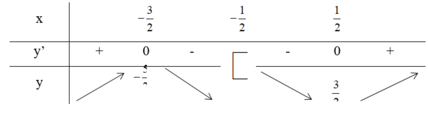
Vậy để bpt có nghiệm trong  - ∞ ; - 1 ⇒ m < - 5 2

Đáp án C

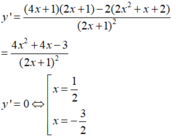
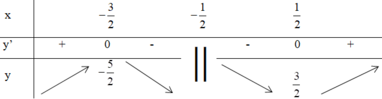
Vậy để bpt có nghiệm trong  ( − ∞ ; − 1 ) ⇒ m < − 5 2