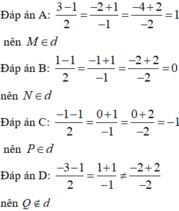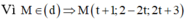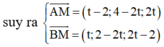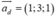Trong không gian tọa độ cho đường thẳng d : x - 3 2 = y + 2 1 = z + 1 - 1 và mặt phẳng (P): x + y + z + 2 = 0. Gọi M là giao điểm của d và (P). Viết phương trình đường thẳng ∆ nằm trong mặt phẳng P , vuông góc với d đồng thời thỏa mãn khoảng cách từ M tới ∆ bằng 42
A.
x + 5 2 = y + 2 - 3 = z + 5 1 x + 3 2 = y + 4 - 3 = z - 5 1
B.
x - 5 - 2 = y + 2 - 3 = z + 5 1 x + 3 2 = y + 4 - 3 = z - 5 1
C.
x - 5 2 = y + 2 - 3 = z + 5 1 x + 3 2 = y + 4 3 = z - 5 1
D.
x - 5 2 = y + 2 - 3 = z + 5 1 x + 3 2 = y + 4 - 3 = z - 5 1
suy ra
A
M
→
=
(
t
-
2
;
4
-
2
t
;
2
t
)
B
M
→
=
(
t
;
2
-
2
t
;
2
t
-
2
)
