Trong không tọa độ Oxyz, xét mặt phẳng ( α ) đi qua điểm A(2;1;3) đồng thời cắt các tia Ox, Oy, Oz lần lượt tại M,N,P sao cho tứ diện OMNP có thể tích nhỏ nhất. Giao điểm của đường thẳng d : x = 2 + t y = 1 - t z = 4 + t với mặt phẳng có tọa độ là:
Những câu hỏi liên quan
Trong không gian tọa độ Oxyz, cho điểm A(5;4;3). Gọi
(
α
)
là mặt phẳng đi qua các hình chiếu của A lên các trục tọa độ. Phương trình của mặt phẳng
(
α
)
là: A.
12
x
+
15
y
+
20
z
-
10...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho điểm A(5;4;3). Gọi ( α ) là mặt phẳng đi qua các hình chiếu của A lên các trục tọa độ. Phương trình của mặt phẳng ( α ) là:
A. 12 x + 15 y + 20 z - 10 = 0
B. 12 x + 15 y + 20 z + 60 = 0
C. x 5 + y 4 + z 3 = 1
D. x 5 + y 4 + z 3 - 60 = 0
Đáp án C
Gợi A’, B’ C’ hình chiếu của A lên Ox, Oy, Oz. Ta có:
A'(5;0;0), B'(0;4;0), C(0;0;3) => PT ( α ) : x 5 + y 4 + z 3 = 1
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho điểm
A
5
;
4
;
3
.
Gọi
α
là mặt phẳng đi qua các hình chiếu của A lên các trục tọa độ. Phương trình của mặt phẳng là: A.
12
x
+
15
y
+
20
z
-
10
...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho điểm A 5 ; 4 ; 3 . Gọi α là mặt phẳng đi qua các hình chiếu của A lên các trục tọa độ. Phương trình của mặt phẳng là:
A. 12 x + 15 y + 20 z - 10 = 0
B. 12x + 15y + 20z + 60 = 0
C. x 5 + y 4 + z 3 = 1
D. x 5 + y 4 + z 3 - 60 = 0
Trong không gian Oxyz, cho điểm A(2; –1;1). Phương trình mặt phẳng (α) đi qua hình chiếu của điểm A trên các trục tọa độ là A.
x
2
y
-
1
z
1
0
B. ...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(2; –1;1). Phương trình mặt phẳng (α) đi qua hình chiếu của điểm A trên các trục tọa độ là
A. x 2 = y - 1 = z 1 = 0
B. x 2 + y - 1 + z 1 = 1
C. x 2 + y 1 + z 1 = 1
D. x 2 + y - 1 + z 1 = - 1
Đáp án B
Phương pháp:
Hình chiếu của điểm M(x0;y0;z0) trên trục Ox là điểm M1(x0;0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oy là điểm M2(0;y0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oz là điểm M3(0;0;z0)
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c), (a,b,c ≠ 0) là: x a + y b + z c = 1
Cách giải: Hình chiếu của điểm A(2; –1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0; –1;0), (0;0;1)
Phương trình mặt phẳng (α): x 2 + y - 1 + z 1 = 1
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm A(2;-1;1). Phương trình mặt phẳng
α
đi qua hình chiếu của điểm A trên các trục tọa độ là A.
x
2
+
y
-
1
+
z
1
0
B. ...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(2;-1;1). Phương trình mặt phẳng α đi qua hình chiếu của điểm A trên các trục tọa độ là
A. x 2 + y - 1 + z 1 = 0
B. x 2 + y - 1 + z 1 = 1
C. x 2 + y 1 + z 1 = 1
D. x 2 + y - 1 + z 1 = - 1
Đáp án B
Phương pháp:
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Ox là điểm M 1 ( x 0 ; 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oy là điểm M 2 ( 0 ; y 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oz là điểm M 3 ( 0 ; 0 ; z 0 )
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) (a,b,c ≠ 0 ) là
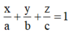
Cách giải: Hình chiếu của điểm A(2;-1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0;-1;0),(0;0;1).
Phương trình mặt phẳng α : x 2 + y - 1 + z 1 = 1
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến (2; 3; 5). Phương trình mặt phẳng (α) là: A. 2x + 3y + 5z - 160 B. x - 2y + 4z - 160 C. 2x + 3y + 5z + 160 D. x - 2y + 4z0.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến 
=(2; 3; 5). Phương trình mặt phẳng (α) là:
A. 2x + 3y + 5z - 16=0
B. x - 2y + 4z - 16=0
C. 2x + 3y + 5z + 16=0
D. x - 2y + 4z=0.
Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
y
-
3
z
+
10
0
và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng
α
có phương trình là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng α có phương trình là:
Trong không gian với hệ tọa độ Oxyz, phương trình
(
α
)
mặt phẳng
A
(
0
;
−
1
;
0
)
,
B
(
2
;
0
;
0
)
;
C
(
0
;
0
;
3
)
đi qua điểm là A.
x
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình ( α ) mặt phẳng A ( 0 ; − 1 ; 0 ) , B ( 2 ; 0 ; 0 ) ; C ( 0 ; 0 ; 3 ) đi qua điểm là
A. x 2 + y 1 + z 3 = 1.
B. x 2 + y − 1 + z 3 = 0.
C. x − 1 + y 2 + z 3 = 1.
D. x 2 + y − 1 + z 3 = 1.
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng
α
đi qua điểm A(0;-1;0), B(2;0;0), C(0;0;3) là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng α đi qua điểm A(0;-1;0), B(2;0;0), C(0;0;3) là
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng
α
:
x
−
4
y
+
z
0
. Viết phương trình mặt phẳng
β
đi qua A và song song với mặt phẳng
α
. A.
x
−
4
y
+
z
−
4
0
B.
x
−
4...
Đọc tiếp
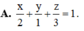
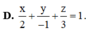
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng α : x − 4 y + z = 0 . Viết phương trình mặt phẳng β đi qua A và song song với mặt phẳng α .
A. x − 4 y + z − 4 = 0
B. x − 4 y + z + 4 = 0
C. 2 x + y + 2 z − 10 = 0
D. 2 x + y + 2 z + 10 = 0
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng
α
đi qua điểm
A
1
;
2
;
-
1
sao cho khoảng cách từ
B
1
;
0
;
0
đến mặt phẳng
α
lớn nhất. A.
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng α đi qua điểm A 1 ; 2 ; - 1 sao cho khoảng cách từ B 1 ; 0 ; 0 đến mặt phẳng α lớn nhất.
A. 2 y + z - 3 = 0
B. 2 y - z = 0
C. 2 y - z - 5 = 0
D. x + 2 y - z - 6 = 0
