Trong không gian Oxyz, cho ba điểm A(3;5;-1), B(7;x;1), C(9;2;y). Để A, B, C thẳng hàng thì giá trị x+y bằng
A. 5
B. 6
C. 4
D. 7
Những câu hỏi liên quan
Trong không gian Oxyz cho điểm A(3;-4;3) . Tổng khoảng cách từ A đến ba trục tọa độ bằng
A. 34
B. 10
C. 34 2
D. 10 + 3 2
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là:
A
.
x
8
3
+
26
t
y
5...
Đọc tiếp
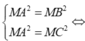
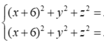
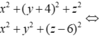
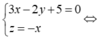
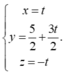
Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là:
A . x = 8 3 + 26 t y = 5 3 + 22 t z = 4 3 + 27 t
B . x = 4 + 26 t y = 2 + 22 t z = 9 4 + 27 t
C . x = 11 6 y = 1 6 + 22 t z = 27 t
D . x = 4 + 26 t y = 2 + 38 t z = 9 4 + 27 t
Chọn B
Gọi I là trung điểm của AB suy ra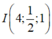 
và (P) là mặt phẳng trung trực của đoạn AB.
Mặt phẳng (P) đi qua I và nhận 
làm vec tơ pháp tuyến có phương trình là:
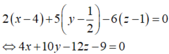
Gọi J là trung điểm của AC suy ra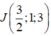 
và (Q) là mặt phẳng trung trực của đoạn AC
Mặt phẳng (Q) đi qua J và nhận 
làm vec tơ pháp tuyến có phương trình là:
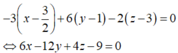
Khi đó d = (P) ∩ (Q)
Ta có d có vectơ chỉ phương 
và đi qua M là nghiệm của hệ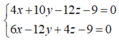 
, ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy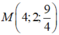 
Phương trình tham số của d là: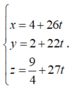 
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm A(2;1;-3), B(4;2;-6), C(10;5;-15). Khẳng định nào sau đây là đúng? A. A, B, C là ba đỉnh của một tam giác B.
BC
→
-
3
BA
→
C.
AC
→
-
4
AB
→
D.
CB
→...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(2;1;-3), B(4;2;-6), C(10;5;-15). Khẳng định nào sau đây là đúng?
A. A, B, C là ba đỉnh của một tam giác
B. BC → = - 3 BA →
C. AC → = - 4 AB →
D. CB → = 3 AB →
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là: A. 2x -3y +6z 0 B. 4y + 2z -3 0 C. 3x + 2y +1 0 D. 2y + z -3 0
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là:
A. 2x -3y +6z =0
B. 4y + 2z -3 =0
C. 3x + 2y +1 =0
D. 2y + z -3 =0
Đáp án A
(ABC) qua A(3; -2; -2) và có véc tơ pháp tuyến
Đúng 0
Bình luận (0)
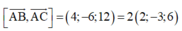
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
A. 3 2
B. 7 2
C. 5 2
D. 9 2
Trong không gian với hệ toạ độ Oxyz, cho ba điểm
A
3
;
−
2
;
−
2
,
B
3
;
2
;
0
,
C
0
;
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A 3 ; − 2 ; − 2 , B 3 ; 2 ; 0 , C 0 ; 2 ; 1 . Phương trình mặt phẳng (ABC) là:
A. 2 x − 3 y + 6 z = 0
B. 4 y + 2 z − 3 = 0
C. 3 x + 2 y + 1 = 0
D. 2 y + z − 3 = 0
Đáp án A
A B → = 0 ; 4 ; 2 , A C → = − 3 ; 4 ; 3
A B C qua A 3 ; − 2 ; − 2 và có véc tơ pháp tuyến A B → , A C → = 4 ; − 6 ; 12 = 2 2 ; − 3 ; 6
⇒ A B C : 2 x − 3 y + 6 z = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
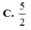
| Trong không gian Oxyz,cho ba điểm A(1;-1;3), B(4;3;-1) và C(3;-3;2). Viết phương trình |
| đường thẳng qua A và song song BC. |
Ta có: \(\overrightarrow{BC}=\left(-1;-6;3\right)\)
Đường thẳng song song với \(BC\) nên nó nhận \(\overrightarrow{BC}\) làm VTCP
\(\Rightarrow\) Phương trình tham số của đường thẳng đi qua \(A\) và song song với \(BC\) là: \(\left\{{}\begin{matrix}x=1-t\\y=-1-6t\\z=3+3t\end{matrix}\right.\quad\left(t\in R\right)\).
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn điểm A(-1;2;0), B(3;1;0), C(0;2;1), D(1;2;2). Trong đó có ba điểm thẳng hàng là
A. A, C, D
B. A, B, D
C. B, C, D
D. A, B, C
