Gọi z 1 , z 2 là hai trong các số phức thỏa mãn z - 1 + 2 i = 5 và z 1 - z 2 = 8 . Tìm môđun của số phức w = z 1 + z 2 - 2 + 4 i ?
A. w = 6
B. w = 16
C. w = 10
D. w = 13
Những câu hỏi liên quan
Trong tập các số phức gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
với
z
2
có phần ảo dương. Cho số phức z thỏa mãn |z-
z
1
| 1 Giá trị nhỏ nhất của P |z...
Đọc tiếp
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình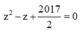 
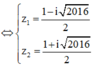
Ta có 
Vật giá trị nhỏ nhất của biểu thức P là 
Đúng 0
Bình luận (0)
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với ...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Đáp án A
Phương pháp.
Giả sử 
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa 
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm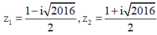 
Giả sử 
. Từ 
ta suy ra
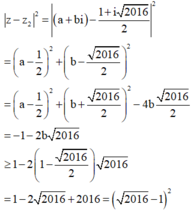
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của 
là
2016
-
1
Đạt được khi và chỉ khi 
Đúng 0
Bình luận (0)
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với
z
2
có thành phần ảo dương. Cho số phức z thỏa mãn
z
-
z...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
Trong tập các số phức gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
−
z
+
2017
4
0
với
z
2
có phần ảo dương. Cho số phức z thỏa mãn
z
−
z
1...
Đọc tiếp
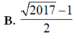
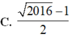
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 − z + 2017 4 = 0 với z 2 có phần ảo dương. Cho số phức z thỏa mãn z − z 1 = 1. Giá trị nhỏ nhất của P = z − z 2 là
A. 2016 − 1
B. 2017 − 1
C. 2017 − 1 2
D. 2016 − 1 2
Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1
Đúng 0
Bình luận (0)
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với
z
2
có thành phần ảo dương. Cho số phức z thỏa mãn |
z
-
z
1
|1 Giá trị nhỏ nhất của P|...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn | z - z 1 |=1 Giá trị nhỏ nhất của P=| z - z 2 |là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Trong các số phức z thỏa mãn
z
−
2
−
3
i
2
, gọi
z
0
là số phức có môđun nhỏ nhất. Khi đó
z
0
bằng A.
z
0
15
−
4...
Đọc tiếp
Trong các số phức z thỏa mãn z − 2 − 3 i = 2 , gọi z 0 là số phức có môđun nhỏ nhất. Khi đó z 0 bằng
A. z 0 = 15 − 4 13
B. z 0 = 18 − 4 13
C. z 0 = 2 4 − 13
D. z 0 = 17 − 4 13
Trong các số phức z thỏa mãn
z
+
3
+
4
i
2
, gọi
z
0
là số phức có mô đun nhỏ nhất. Khi đó A.
z
0
7
B.
z
0
2 C.
z
0...
Đọc tiếp
Trong các số phức z thỏa mãn z + 3 + 4 i = 2 , gọi z 0 là số phức có mô đun nhỏ nhất. Khi đó
A. z 0 = 7
B. z 0 =2
C. z 0 = 3
D. Không tồn tại số phức z 0
Gọi
z
1
,
z
2
là hai trong các số phức z thỏa mãn
z
-
3
+
5
i
5
và
z
1
-
z
2
6
. Tìm môđun của s...
Đọc tiếp
Gọi z 1 , z 2 là hai trong các số phức z thỏa mãn z - 3 + 5 i = 5 và z 1 - z 2 = 6 . Tìm môđun của số phức w = z 1 + z 2 - 6 + 10 i
Kí hiệu A là tập hợp các số phức z đồng thời thỏa mãn hai điều kiện
z
-
1
34
và
z
+
1
+
m
i
z
+
m
+
2
i
(trong đó m ϵ R ). Gọi ...
Đọc tiếp
Kí hiệu A là tập hợp các số phức z đồng thời thỏa mãn hai điều kiện z - 1 = 34 và z + 1 + m i = z + m + 2 i (trong đó m ϵ R ). Gọi z 1 ; z 2 là hai số phức thuộc tập hợp A sao cho z 1 - z 2 là lớn nhất. Khi đó, hãy tính giá trị của z 1 + z 2
A. z 1 + z 2 = 10
B. z 1 + z 2 = 2
C. z 1 + z 2 = 2
D. z 1 + z 2 = 130
