Xét số phức z = a + b i a , b ∈ R thỏa mãn điều kiện z - 4 - 3 i = 5 . Tính P=a+b khi biểu thức |z+1-3i|+|z-1+i| đạt giá trị lớn nhất.
A. P=10
B. P=4
C. P=6
D. P=8
Xét các số phức z = a + bi (a,b ϵ R) thỏa mãn z - 4 - 3 i = z - - 2 + i . Tính P = a 2 + b 2 khi z + 1 - 3 i + z - 1 + i đạt giá trị nhỏ nhất.
A. P = 293/9
B. P = 449/32
C. P = 481/32
D. P = 137/9
Xét các số phức z = a + b i , ( a , b ∈ R ) thỏa mãn 4 ( z - z ¯ ) - 15 i = i ( z + z ¯ - 1 ) 2 . Tính F = - a + 4 b khi z - 1 2 + 3 i đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()
Xét các số phức z = a + b i a , b ∈ R thỏa mãn |z-4-3i|=2. Khi |z+1-3i|+|z-1+i| đạt giá trị lớn nhất, giá trị của a – 2b bằng
A. 1
B. -2
C. - 5
D. -1
Với ![]()
![]() Khi đó
Khi đó
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
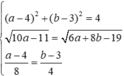
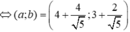
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
![]()
![]()
![]()
Khi đó
![]()
![]()
![]()
![]()
![]()
Khi đó a-2b![]()
Chọn đáp án B.
Xét các số phức z = a + bi, (a,b ∈ R) thỏa mãn đồng thời hai điều kiện z = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2b là:
A. P = - 61 10
B. P = - 252 50
C. P = - 41 5
D. P = - 18 5
Đáp án A.
Phương pháp:
Từ z = z ¯ + 4 - 3 i tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z = x + yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất ó MA = MB
Cách giải: Gọi z = x + ui ta có:
![]()
![]()
![]()
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất.
Ta có: ![]() dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có 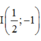 và
A
B
→
=
3
;
-
4
và
A
B
→
=
3
;
-
4
Phương trình đường trung trực của AB là 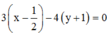
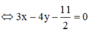
Để (MA + MB)min ó Tọa độ điểm M là nghiệm của hệ phương trình
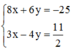
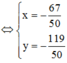
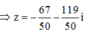

Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left|z_1+3+2i\right|=1\) và \(\left|z_2+2-i\right|=1\). Xét các số phức \(z=a+bi\), (\(a,b\in R\)) thỏa mãn \(2a-b=0\). Khi biểu thức \(T=\left|z-z_1\right|+\left|z-2z_2\right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P=a^2+b^2\) bằng?
Cho số phức z = a + b i a , b ∈ R Nhận xét nào sau đây luôn đúng?
![]()
![]()
![]()
![]()
Cho số phức z = a + b i a , b ∈ R Nhận xét nào sau đây luôn đúng?
A . z 2 ≤ a + b
B . z 2 ≥ a + b
C . z ≤ 2 a + b
D . z ≤ 2 a + b
Xét các số phức z=a+bi ( a , b ∈ R ) thỏa mãn z - 3 - 2 i = 2 . Tính a+b khi z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Xét các số phức z=a+bi z = a + b i ( a , b ∈ R ) thỏa mãn z - 3 + 3 i = 2 . Tính P=a+b khi z - 1 + 3 i + z - 3 + 5 i đạt giá trị lớn nhất
A. 2
B. – 2
C. 8
D. – 8