Hình hộp chữ nhật ABCDA’B’C’D’ có AB = a, AD = a 2 và khoảng cách (D,(AD'C)) = 2 a 3 . Tính AA’.
A. AA' = a 3
B. AA' = a 3
C. AA' = a
D. AA' = a 3
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB = AD = a, AA' = a 2 . Tính khoảng cách h từ D xuống mặt phẳng (BCD').
A. h = a 2 3
B. h = a 2 3
C. h = a 3
D. h = a 2
Cho hình lăng trụ ABCDA’B’C’D’ có đáy ABCD là hình chữ nhật,AB=a,AD=a căn3. Hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) trùng với tâm của ABCD. tính các khoảng cách d(A’D,BC) và d(AB’,BD)
đây là toán 12 11 cũng làm dùm được nhaaa
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = A A ' = a , A D = a 3 . Khoảng cách giữa BD và CD’ bằng
A. a 7
B. 2a
C. a 3 7
D. a 3 5
Đáp án C
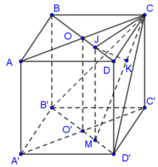
Kẻ CM vuông góc với B’D’; MJ vuông góc với BD; JK vuông góc với CM. Chứng minh khoảng cách giữa BD và CD’ bằng độ dài đoạn JK.
Thật vậy, ta có
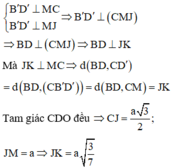
Cho hình hộp chữ nhật ABCD . A ’ B ’ C ’ D ’ có AB = AA ’ = a , AD = a 3 . Khoảng cách giữa BD và CD' bằng
A. a 3 5
B. 2a
C. a 7
D. a 7 3
Đáp án D
Kẻ CM vuông góc với B’D’; MJ vuông góc với BD; JK vuông góc với CM. Chứng minh khoảng cách giữa BD và CD’ bằng độ dài đoạn JK.
Thật vậy, ta có
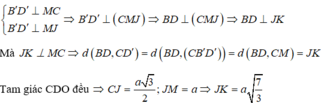
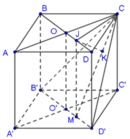
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=AA’=a, AD = a 3 . Khoảng cách giữa BD và CD’ bằng
A. a 7
B. 2a
C. a 3 7
D. a 3 5
Chọn C
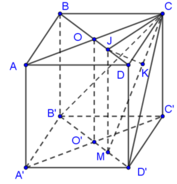
Kẻ CM vuông góc với B’D’; MJ vuông góc với BD; JK vuông góc với CM. Chứng minh khoảng cách giữa BD và CD’ bằng độ dài đoạn JK.
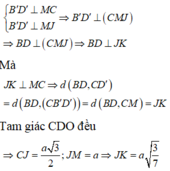
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a ; A D = A A ' = 2 a . Khoảng cách giữa hai đường thẳng AC và D C ' bằng:
A. 6 a 3
B. 3 a 2
C. 3 a 3
D. 3 a 2
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A A ' = a . Gọi M là điểm trên đoạn AD với A D M D = 3 . Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B 'C và y là độ dài khoảng cách từ M đến mặt phẳng A B ' C . Tính giá trị xy
A. 5 a 5 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2
Đáp án B
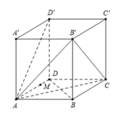
Ta có d D ; A B ' C = d B ; A B ' C mà A M A D = 3 4
Và 1 d 2 B ; A B ' C = 1 A B 2 + 1 B C 2 + 1 B B ' ⇒ d M ; A B ' C = a 2 .
Gọi E, F lần lượt là trung điểm của AD’, B’C.
Suy ra EF là đoạn vuông góc chung cuả AD’, B’C.
Do đó d A D ' ; B ' C = E F = A B = a . Vậy x y = a . a 2 = a 2 2 .
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = a , A A ' = a 3 . Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (B'MC) bằng
A. a 21 7
B. 2 a 21 7
C. 3 a 21 7
D. a 21 14
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)