Cho hàm số f(x) có đạo hàm trên - 1 ; + ∞ .Biết đẳng thức 2 f x + x 2 - 1 f ' x = x x + 1 2 x 2 + 3 được thỏa mãn ∀ x ∈ - 1 ; + ∞ . Tính giá trị f(0).
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D.Chưa đủ dữ kiện tính ![]() .
.
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) . Hàm số f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 . Hàm số đồng biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Hàm số f(x) có đạo hàm trên là hàm số f'(x). Biết đồ thị hàm số f'(x) được cho như hình vẽ. Hàm số f(x) nghịch biến trên khoảng
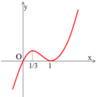
A. 0 ; + ∞
B. 1 3 ; 1
C. − ∞ ; 1 3
D. − ∞ ; 0
Đáp án D
f ' x < 0 ⇔ x < 0 do đó hàm số nghịch biến trên − ∞ ; 0
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x) .
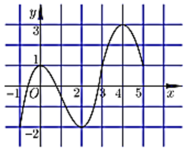
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A (-3 ; -2)
B. (- 2 ; -1)
C. (- 1 ; 0)
D. (0 ; 2)
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng

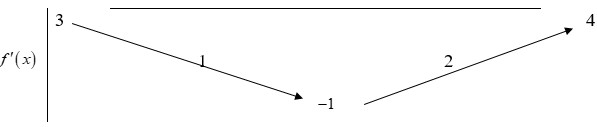
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
Cho hàm số f(x) có đạo hàm f’(x) = (x – 1)(x2 – 3)(x4 – 1) liên tục trên R.Tính số điểm cực trị của hàm số y=f(x)
A. 3
B. 2
C. 4
D. 1
Đáp án A
Phương pháp giải:
Giải phương trình f’ bằng 0, tìm nghiệm và lập bảng biến thiên xét điểm cực trị
Lời giải:
Ta có ![]()
![]()
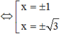
Dễ thấy f’(x) đổi dấu khi đi qua 3 điểm ![]() => Hàm số có 3 điểm cực trị.
=> Hàm số có 3 điểm cực trị.
Cho hàm số f(x) liên tục trên ℝ và có đạo hàm f'(x) = (x+1) x - 2 2 x - 3 3 . Hỏi hàm số f(x) có mấy điểm cực trị?
A. 2.
B. 3.
C. 1.
D. 5.
Chọn A.
Ta có 
Bảng biến thiên

Do đó hàm số f(x) có hai điểm cực trị.
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 ( x 2 - 1 ) , ∀ x ∈ R . Hàm số y = 2 f ( - x ) đồng biến trên khoảng
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f'(x)= x ( x - 1 ) 2 ( x + 1 ) 2 . Hàm số đã cho có bao nhiêu điểm cực trị
A. Có đúng 3 điểm cực trị
B. Không có điểm cực trị
C. Có đúng 1 điểm cực trị
D. Có đúng 2 điểm cực trị