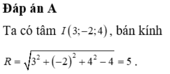Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là

Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
(
S
)
:
(
x
-
5
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
9
. Bán kính R của mặt cầu (S) là A. 3 B. 6 C. 9 D. 18
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : ( x - 5 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 9 . Bán kính R của mặt cầu (S) là
A. 3
B. 6
C. 9
D. 18
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²9. Tính bán kính R của mặt cầu (S). A. R18 B. R9 C. R3 D. R6.
Đọc tiếp
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²=9. Tính bán kính R của mặt cầu (S).
A. R=18
B. R=9
C. R=3
D. R=6.
Đáp án C
Mặt cầu (S) có tâm I(a; b; c) và bán kính R thì có phương trình (x-a)²+(y-b)²+(z-c)²=R².
Theo đề bài ta có R²=9=> R=3.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ): ( x-5 )²+( y-1 )²+( z+2 )²16. Tính bán kính của (S). A. 4 B. 16 C. 7 D. 5.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ): ( x-5 )²+( y-1 )²+( z+2 )²=16. Tính bán kính của (S).
A. 4
B. 16
C. 7
D. 5.
Đáp án A
Bán kính của mặt cầu ( S ) là R=√16 =4.
Đúng 0
Bình luận (0)
#2H3Y1-3~Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x+1)²+(y-2)²+(z-1)²9. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S). A. I(-1;2;1) và R3 B. I(-1;2;1) và R9 C. I(1;-2;-1) và R3 D. I(1;-2;-1) và R9.
Đọc tiếp
#2H3Y1-3~Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x+1)²+(y-2)²+(z-1)²=9. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).
A. I(-1;2;1) và R=3
B. I(-1;2;1) và R=9
C. I(1;-2;-1) và R=3
D. I(1;-2;-1) và R=9.
Đáp án A
Mặt cầu (S) có tâm I(-1;2;1) và bán kính R=√9=3.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
5
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
9
. T...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 5 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 9 . Tính bán kính R của (S)?
A. R=3
B. R=18
C. R=9
D. R=6
Đáp án A
Từ phương trình mặt cầu (S) ⇒ bán kính R= 9 =3
Đúng 0
Bình luận (0)
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2
4
. Tìm tọa độ tâm I và bán kính R của mặt cầu đó A. I(-1;2;3), R2 B. I(-1;2;-3), R...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó
A. I(-1;2;3), R=2
B. I(-1;2;-3), R=4
C. I(1;-2;3); R=2
D. I(1;-2;3), R=4
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x bán kính R9 có phương trình là A.
(
x
+
4
)
2
+
(
y
-
5
)
2
+
(
z
+
6
)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x bán kính R=9 có phương trình là
A. ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 9
B. ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 81
C. ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 9
D. ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 81
Trong không gian với hệ tọa độ oxyz, cho mặt cầu (S) :
x
2
+
(
y
+
2
)
2
+
(
z
-
2
)
2
8
. Tính bán kính R của (S) A. R8 B. R2 C. R4 D. R64
Đọc tiếp
Trong không gian với hệ tọa độ oxyz, cho mặt cầu (S) : x 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 8 . Tính bán kính R của (S)
A. R=8
B. R=2
C. R=4
D. R=64
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-20. Tìm tọa độ tâm I và tính bán kính R của (S). A. Tâm I(-1;2;-3) và bán kính R4 B. Tâm I(1;-2;3) và bán kính R4 C. Tâm I(-1;2;3) và bán kính R4 D. Tâm I(1;-2;3) và bán kính R16.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-2=0. Tìm tọa độ tâm I và tính bán kính R của (S).
A. Tâm I(-1;2;-3) và bán kính R=4
B. Tâm I(1;-2;3) và bán kính R=4
C. Tâm I(-1;2;3) và bán kính R=4
D. Tâm I(1;-2;3) và bán kính R=16.
Đáp án A
Ta có (S): (x+1)²+(y-2)²+(z+3)²=16.
Do đó mặt cầu (S) có tâm I(-1;2;-3) và bán kính R=4.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
-
3...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x + 1 2 + y - 3 2 + z - 2 2 = 9 Tọa độ tâm và bán kính của mặt cầu (S) là
A. I(-1;3;2) R =9
B. I(1;-3;-2) R = 9
C. I(-1;3;2) R = 3
D. I(1;3;2) R = 3
Đáp án C
Tọa độ tâm và bán kính mặt cầu (S): I(-1;3;2) R = 3
Đúng 0
Bình luận (0)