Cho hai số phức z 1 , z 2 có điểm biểu diễn lần lượt là M 1 , M 2 cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 − z 2 = 1. Tính giá trị của biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
Cho số phức z và số phức liên hợp của nó z ¯ có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
A . 1 2
B . 2 5
C . 5 34
D . 4 13
Đáp án A
Giả sử ![]()
Ta có M(a;b) và M'(a;-b)
Khi đó ![]()
Suy ra ![]() và
và ![]()
Do 4 điểm M, N, M’, N’ tạo thành hình thang cân nhận Ox làm trục đối xứng nên 4 điểm đó lập thành hình chữ nhật
![]()

Với a = -b, ta có
![]()
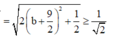
Dấu bằng xảy ra khi 
Với  ta có
ta có 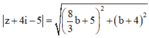
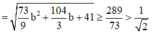
Vậy 
Cho số phức z và số phức liên hợp của nó z có điểm biểu diễn là M, M’. Số phức z . ( 4 + 3 i ) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức | z + 4 i - 5 | .
A. 1 2
B. 2 5
C. 5 34
D. 4 13
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M'. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N'. Biết rằng M, M', N, N' là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z + 4 i - 5 .
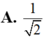
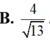
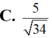
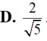
Cho số phức z = 2 + 3i. Gọi M là điểm biểu diễn số phức z, N là điểm biểu diễn số phức z ¯ và P là điểm biểu diễn số phức (1+i)z. Khẳng định nào sau đây là khẳng định sai?
A. M(2;3)
B. M(2;-3)
C. P(1;5)
D. |z| = 13
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z-1+i| = 2 là đường tròn có tâm và bán kính lần lượt là
A. I(-1;1), R = 4
B. I(-1;1), R = 2
C. I(1;-1), R = 2
D. I(1;-1), R = 4
Cho số phức z = 2 + 3i. Gọi M là điểm biểu diễn số phức z, N là điểm biểu diễn số phức z, N và P là điểm biểu diễn số phức (1+i)z. Khẳng định nào sau đây là khẳng định sai?
A. M(2;3)
B. N(2;-3)
C. P(1;5)
D. |z| = 13
Cho các số phức z1 , z2 ,z3 ,z4 , z5 có các điểm biểu diễn lần lượt là A, B , C , D ,E trong mặt phẳng phức tạo thành ngũ giác lồi . Gọi M N P Q lần lượt là trung điểm AB BC CD DE . Gọi I,J lần lượt là trung điểm MP và NQ . Biết I J là điểm biểu diễn hai số phức z=1-i và z=2i và điểm E là z=4-5i Tìm z1
Cho số phức z = 2 + 3 i . Gọi M là điểm biểu diễn số phức z, N là điểm biểu diễn số phức z ¯ và P là điểm biểu diễn số phức 1 + i z . Khẳng định nào sau đây là khẳng định sai?
A. M 2 ; 3 .
B. N 2 ; − 3 .
C. P 1 ; 5 .
D. z = 13 .
Đáp án C.
Ta có: N 2 ; − 3 ; 1 + i z = 1 + i 2 + 3 i = − 1 + 5 i do đó P − 1 ; 5 .