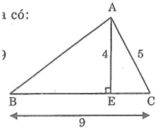
Áp dụng định lý pitago vào tam giác vuông AEC ta có:

AC2=AE2+EC2

=>EC2=AC2-AE2=52-42=25-16=9

=>EC=3M

Ta có: BC = BE + EC

BE = BC – EC = 9 – 3 = 6(m)

Áp dụng định lí pitago vào tam giác vuông AEB, ta có:

AB2=AE2+EB2=42+62=16+36=52

Suy ra: AB = √52(m) ≈7,2m

Hình vẽ: 

Xét \(\Delta ACH\left(\widehat{H}=90^0\right)\)có: 

\(AC^2=AH^2+HC^2\)( định lý py-ta-go )

\(\Rightarrow5^2=4^2+HC^2\)

\(\Rightarrow HC^2=5^2-4^2\)

\(\Rightarrow HC^2=25-16\)

\(\Rightarrow HC^2=9\)

\(\Rightarrow HC=\sqrt{9}\)

\(\Rightarrow HC=3cm\)

Ta có: \(BH+HC=9cm\)

mà \(HC=3cm\left(cmt\right)\)

\(\Rightarrow BH=9-3=6cm\)

Xét \(\Delta AHB\left(\widehat{H}=90^0\right)\)có:
\(AB^2=AH^2+BH^2\)( định lý py-ta-go )

\(\Rightarrow AB^2=4^2+6^2\)

\(\Rightarrow AB^2=16+36\)

\(\Rightarrow AB^2=52\)

\(\Rightarrow AB=\sqrt{52}cm\)

Vậy độ dài cạnh AB là \(\sqrt{52}cm\)

a) Xét tam giác ABC có AD là phân giác

\(\Rightarrow\dfrac{BD}{AB}=\dfrac{DC}{AC}=\dfrac{BD+DC}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{5}{4+6}=\dfrac{5}{10}=\dfrac{1}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{1}{2}.AB=\dfrac{1}{2}.4=2\left(cm\right)\\DC=\dfrac{1}{2}.AC=\dfrac{1}{2}.6=3\left(cm\right)\end{matrix}\right.\)

b) Ta có: DE//AC \(\Rightarrow\widehat{ADE}=\widehat{DAC}\)(so le trong)

Mà \(\widehat{DAC}=\widehat{BAD}\)(AD là phân giác)

\(\Rightarrow\widehat{ADE}=\widehat{BAD}\) => Tam giác ADE cân tại E => AE=DE

c) Xét tam giác ABC có:

DE//AC \(\Rightarrow\dfrac{DE}{AC}=\dfrac{BD}{BC}\Rightarrow DE=\dfrac{BD.AC}{BC}=\dfrac{2.6}{5}=2,4\left(cm\right)\)

Mà AE=DE \(\Rightarrow AE=DE=2,4cm\)

cho mik xin cái hình 

bn tự vẽ hay là bài họ cho