Mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với 3 mặt phẳng .Bán kính mặt cầu (S) là
Đọc tiếp
Mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với 3 mặt phẳng 
.Bán kính mặt cầu (S) là
Những câu hỏi liên quan
Mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với 3 mặt phẳng
(
α
)
:
x
1
,
(
β
)
:
y
-
1
,
γ
:
z
1
. Bán kính mặt cầu (S) là A.
3
3
B. 1 C. 3 D.
2
3
Đọc tiếp
Mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với 3 mặt phẳng ( α ) : x = 1 , ( β ) : y = - 1 , γ : z = 1 . Bán kính mặt cầu (S) là
A. 3 3
B. 1
C. 3
D. 2 3
Trong không gian Oxyz, cho mặt cầu (S): (x-1)2+ (y-2)2+ z225 và một điểm A(a,b,c) nằm trên mặt cầu (S). Từ A vẽ ba tia đôi một vuông góc với nhau cắt mặt cầu (S) tại điểm thứ hai là M, N, P. Biết rằng mặt phẳng (MNP) luôn đi qua một điểm cố định K(1;1;3). Giá trị của biểu thức a + 7b + c bằng A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)2+ (y-2)2+ z2=25 và một điểm A(a,b,c) nằm trên mặt cầu (S). Từ A vẽ ba tia đôi một vuông góc với nhau cắt mặt cầu (S) tại điểm thứ hai là M, N, P. Biết rằng mặt phẳng (MNP) luôn đi qua một điểm cố định K(1;1;3). Giá trị của biểu thức a + 7b + c bằng
A. 3
B. 4
C. 6
D. 9
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là: A.
x
2
+
y
2
+
z
2
+ 2x - y - 2z 0 B.
x
2
+
y...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là:
A. x 2 + y 2 + z 2 + 2x - y - 2z = 0
B. x 2 + y 2 + z 2 + 4x + 2y - 4z = 0
C. x 2 + y 2 + z 2 + 4x - 2y + 4z = 0S
D. x 2 + y 2 + z 2 + 4x - 2y - 4z = 0
Đáp án D
Phương trình tổng quát của mặt cầu (S) có dạng x 2 + y 2 + z 2 - 2ax - 2by - 2cz + d = 0 với a 2 + b 2 + c 2 - d > 0
Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0
A(-4; 0; 0) ∈ (S) ⇔ ( - 4 ) 2 + 0 2 + 0 2 - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2
B(0; 2; 0) ∈ (S) ⇔ 0 2 + 2 2 + 0 2 - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1
C(0; 0; 4) ∈ (S) ⇔ 0 2 + 0 2 + 4 2 - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2
Vậy phương trình tổng quát của mặt cầu (S) là: x 2 + y 2 + z 2 + 4x -2y - 4z = 0
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 3
B. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
C. ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 3
D. ( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 9
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
α
:
x
1
,
β
:
y
-
1
,
γ
:
z
1
. Bán kính mặt cầu (S) bằng: A. 3 B. 1 C.
3
2
D.
33
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng α : x = 1 , β : y = - 1 , γ : z = 1 . Bán kính mặt cầu (S) bằng:
A. 3
B. 1
C. 3 2
D. 33
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
α
:
x
1
,
β
:
y
-
1
,
γ
:
z
1
. Bán kính mặt cầu (S) bằng: A. 3 B. 1 C.
3
2
D.
33
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng α : x = 1 , β : y = - 1 , γ : z = 1 . Bán kính mặt cầu (S) bằng:
A. 3
B. 1
C. 3 2
D. 33
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là: A.
(
x
-
1
)
2
+
(
y
+
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là:
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 6
B. ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 24
C. ( x - 4 ) 2 + ( y + 2 ) 2 + ( z + 2 ) 2 = 24
D. ( x + 2 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 6
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên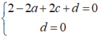 
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
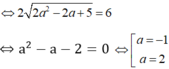
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;6;2), B(3;0;0) và có tâm thuộc mặt phẳng (P):x - y + 2 0. Bán kính mặt cầu (S) có giá trị nhỏ nhất là: A.
534
4
B.
426
6
C.
530
4
D.
218
6
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;6;2), B(3;0;0) và có tâm thuộc mặt phẳng (P):x - y + 2 =0. Bán kính mặt cầu (S) có giá trị nhỏ nhất là:
A. 534 4
B. 426 6
C. 530 4
D. 218 6
Đáp án B
Cách 1: Gọi I(a;b;c) là tâm của mặt cầu (S), vì I ∈ ( P ) ⇒ I ( a ; a + 2 ; c )
Ta có R = I A = I B ⇔ a - 1 2 + a - 4 2 + c - 2 2 = a - 3 2 + a + 2 2 + c 2 ⇔ c = 2 - 2 a
Khi đó R = I A = a - 1 2 + a - 4 2 + 4 a 2 = 6 a 2 - 10 a + 17 = 6 x - 5 6 2 + 77 6 ≥ 462 6
Vậy bán kính nhỏ nhất của mặt cầu (S) là
R
m
i
n
=
462
6
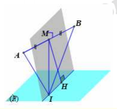
Cách 2: Tham khảo hình bên
Ta có I thuộc giao tuyến mặt phẳng trung trực AB và P ⇒ I M ≥ M H
⇒ R ≥ H A ⇒ R m i n = H A với H là hình chiếu của M trên giao tuyến ⇒ R m i n = 462 6
Đúng 0
Bình luận (0)