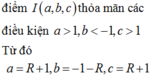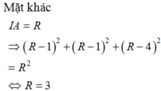Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
α
:
x
1
,
β
:
y
-
1
,
γ
:
z
1
. Bán kính mặt cầu (S) bằng: A. 3 B. 1 C.
3
2
D.
33
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng α : x = 1 , β : y = - 1 , γ : z = 1 . Bán kính mặt cầu (S) bằng:
A. 3
B. 1
C. 3 2
D. 33
Trong không gian Oxyz, mặt cầu (S) đi qua điểm A(2-2;5) và tiếp xúc với ba mặt phẳng (P): x1; (Q):y-1 và (R): z1 có bán kính bằng A. 3 B. 1
Đọc tiếp
Trong không gian Oxyz, mặt cầu (S) đi qua điểm A(2'-2;5) và tiếp xúc với ba mặt phẳng (P): x=1; (Q):y=-1 và (R): z=1 có bán kính bằng
A. 3
B. 1
![]()
![]()
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
Đọc tiếp
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
![]()
![]()
![]()
![]()
Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Mặt cầu (S) bán kính bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất kì trên (S), MH là khoảng cách từ M đến mặt phẳng (P). Giá trị lớn nhất của MH là
Đọc tiếp
Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Mặt cầu (S) bán kính bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất kì trên (S), MH là khoảng cách từ M đến mặt phẳng (P). Giá trị lớn nhất của MH là
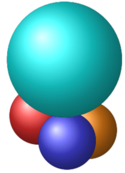
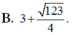
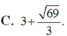
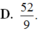
Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)
Đọc tiếp
Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)
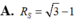
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D. A. 1 B. 2 C. 4 D. Vô số.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 4
D. Vô số.
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn
I
M
3
R
2
. Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng: A. ABR B. ABR
3
C. AB
3
R
2
D. ABR hoặc ABR
3
Đọc tiếp
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C. AB= 3 R 2
D. AB=R hoặc AB=R 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
![]()
![]()
![]()
![]()