Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]. Khi đó số phần tử của S là
A. 11
B. 10
C. Vô số
D. 9
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
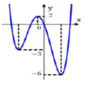
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
A. 9
B. 7
C. 12
D. 18
Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 14 x 2 + 48 x + m - 30 trên đoạn [0;2] không vượt quá 30. Tính tổng tất cả các phần tử của S
A.108
B.120
C.210
D.136
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A.210
B.-195
C.105
D.300
Chọn C
Xét hàm số ![]() trên đoạn
trên đoạn ![]()
Ta có ![]() ;
; 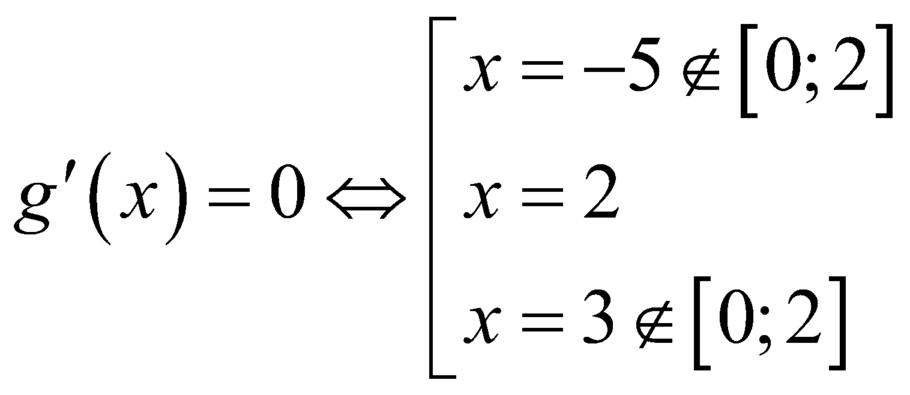
Bảng biến thiên

![]() ;
; ![]() .
.
Để ![]() thì
thì 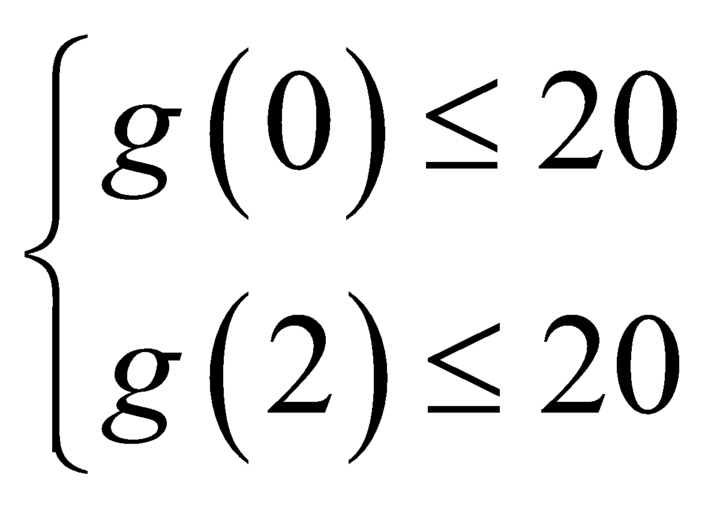
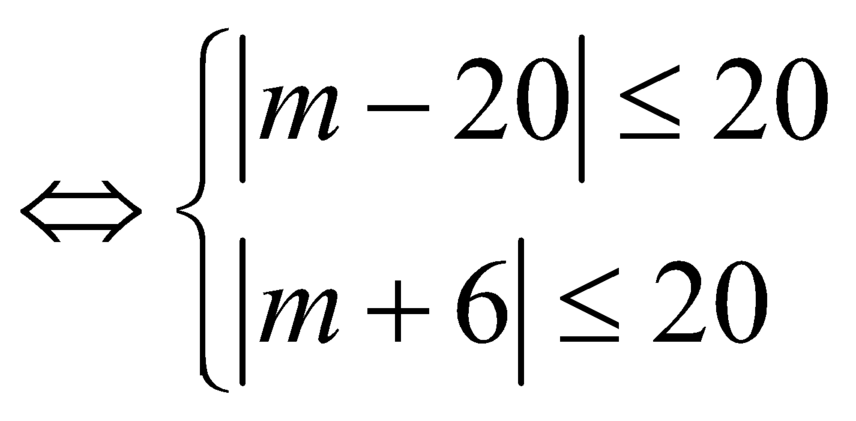
![]() .
.
Mà ![]() nên
nên ![]() .
.
Vậy tổng các phần tử của ![]() là
là ![]() .
.
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng
A. 210
B. -195
C. 105
D. 300
Chọn C
Xét hàm số ![]() trên đoạn [0;2]
trên đoạn [0;2]
![]()
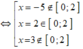
Bảng biến thiên:
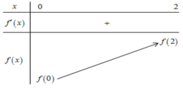
với f(0) = m - 20; f(2) = m + 6
Xét hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2]
+ Trường hợp 1: ![]() Ta có:
Ta có:
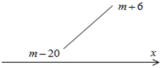
![]()
![]() suy ra không có giá trị m.
suy ra không có giá trị m.
+ Trường hợp 2: ![]() Ta có:
Ta có:

![]()
![]()
Vì m nguyên nên ![]()
+ Trường hợp 3: ![]()
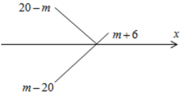
![]()
![]()
Vì m nguyên nên ![]()
Vậy ![]() Tổng các phần tử của S bằng
Tổng các phần tử của S bằng 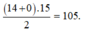
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
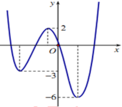
A. 12
B. 15
C. 18
D. 9
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 - m x + 2 m x - 2 trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S.
A. - 8 3
B. 5
C. 5 3
D. -1
Chọn D
Xét hàm số y =
x
2
-
m
x
+
2
m
x
-
2
trên [-1;1] có: 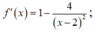
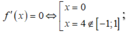
![]()
Bảng biến thiên

Trường hợp 1. ![]() Khi đó
Khi đó
![]()
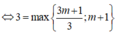
![]()
Trường hợp 2. ![]()
Khả năng 1. 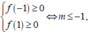
Khi đó ![]()
Khả năng 2 ![]() Khi đó
Khi đó 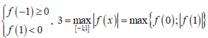
![]() Trường hợp này vô nghiệm.
Trường hợp này vô nghiệm.
Khả năng 3. ![]() Khi đó
Khi đó ![]() Vô nghiệm.
Vô nghiệm.
Vậy có hai giá trị thỏa mãn là ![]() Do đó tổng tất cả các phần tử của S là -1.
Do đó tổng tất cả các phần tử của S là -1.
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 − m x + 2 x − 2 trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S.
A. − 8 3
B. 5
C. 5 3
D. -1
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng:
A. 210
B. 105
C. -195
D. 300
Đáp án B
Xét hàm số f x = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên [0;2] có f ' x = 0 ⇔ x = 2
Tính f 0 = m - 20 ; f 2 = m + 6 → m a x 0 ; 2 y = m a x [ 0 ; 2 ] f x = m - 20 ; m + 6
TH1. Với m a x 0 ; 2 y = m - 20 ⇒ m - 20 ≥ m + 6 m - 20 ≤ 20 ⇔ m ≤ 7 - 20 ≤ m ≤ 20 ⇔ 0 ≤ m ≤ 7
TH2. Với m a x 0 ; 2 y = m + 6 ⇒ m - 20 ≤ m + 6 m + 6 ≤ 20 ⇔ m ≥ 7 - 20 ≤ m + 6 ≤ 20 ⇔ 7 ≤ m ≤ 14
Kết hợp với m ∈ ℤ , ta được m = 0 ; 1 ; 2 ; . . . ; 14 → ∑ m = 105 .