Cho số phức z = 1-3i Tính P = ( z - z ¯ ) 2
A. P = 4
B. P = -4
C. P = 36
D. P = -36
Những câu hỏi liên quan
Bài tập số 4: Tìm số phức liên hợp overline{Z} và tính modun (|z|) của số phức sau. a, z 2 + 3i b, zleft(2+3iright)^3 c, zdfrac{2+3i}{1-2i} d, zsqrt{2}-dfrac{4}{3}i
Đọc tiếp
Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.
a, z = 2 + 3i b, \(z=\left(2+3i\right)^3\)
c, \(z=\dfrac{2+3i}{1-2i}\) d, \(z=\sqrt{2}-\dfrac{4}{3}i\)
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tính giá trị nhỏ nhất của
z
-
w...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Cho số phức z thỏa mãn z-(1+3i) z ¯ = -3+8i. Tính |z|.
Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+
3
i
-...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính m i n w , với w = z - 2 + 2 i .
A. m i n w = 3 2
B. m i n w = 2
C. m i n w = 1
D. m i n w = 1 2
Cho số phức z thỏa mãn
z
+
1
-
i
z
-
3
i
. Tính môđun lớn nhất
w
m
a
x
của số phức
w
1
2
A.
w...
Đọc tiếp
Cho số phức z thỏa mãn z + 1 - i = z - 3 i . Tính môđun lớn nhất w m a x của số phức w = 1 2
A. w m a x = 7 5 10
B. w m a x = 2 5 7
C. w m a x = 4 5 7
D. w m a x = 9 5 10
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính min |w|, với w = z - 2 + 2 i
Cho số phức z thỏa mãn
|
z
-
1
-
3
i
|
13
. Gọi m, M lần lượt là giá trị nhỏ nhất và lớn nhất của biểu thức
P
|
z
+
2
|
2
-
|
z...
Đọc tiếp
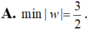
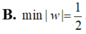
Cho số phức z thỏa mãn | z - 1 - 3 i | = 13 . Gọi m, M lần lượt là giá trị nhỏ nhất và lớn nhất của biểu thức P = | z + 2 | 2 - | z - 3 i | 2 . Tính A= m+M.
A. A = 10.
B. A = 25.
C. A = 34.
D. A = 40
Cho số phức z thỏa mãn \(\left(1+i\right)z+2\overline{z}=2\)
Tính môdun của số phức \(\omega=z+2+3i\)
Giả sử: \(z=x+yi\) \((x;y\in|R)\)
Ta có: \((1+i)z+2\overline{z}=2\)
<=> \((1+i)(x+yi)+2(x-yi)=2\)
<=> \(x+yi+xi-y+2x-2yi-2=0\)
<=> \((3x-y-2)+(x-y)i=0\)
<=> \(\begin{align} \begin{cases} 3x-y&=2\\ x-y&=0 \end{cases} \end{align}\)
<=> \(\begin{align} \begin{cases} x&=1\\ y&=1 \end{cases} \end{align}\)
=> \(z=1+i\)
Ta có: \(\omega=z+2+3i \)
\(=1+i+2+3i\)
\(=3+4i\)
=> \(|\omega|=\sqrt{3^2+4^2}=5\)
Đúng 0
Bình luận (0)
Đặt \(z=a+bi\left(a,b\in R\right)\)
Theo bài ta có : \(\begin{cases}3a-b=2\\a-b=0\end{cases}\) \(\Leftrightarrow\begin{cases}a=1\\b=1\end{cases}\) nên \(z=1+i\)
Khi đó \(\omega=z+2+3i=1+i+2+3i=3+4i\)
Vậy \(\left|\omega\right|=\sqrt{3^2+4^2}=5\)
Đúng 0
Bình luận (0)
