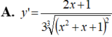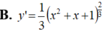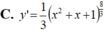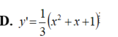Tính đạo hàm của hàm số y= (x2-x+1)1/3
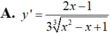
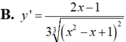
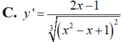
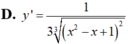
Tính đạo hàm của hàm số sau: y = (x2 – x + 1)3 .(x2 + x + 1)2
A. y’ = (x2 – x + 1)2[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)]
B. y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + (x2 – x + 1)]
C. y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)]
D. y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) – 2(2x + 1)(x2 – x + 1)]
Chọn C.
Đầu tiên sử dụng quy tắc nhân.
y' = [(x2 – x + 1)3]’(x2 + x + 1)2 + [(x2 + x + 1)2]’(x2 – x + 1)3.
Sau đó sử dụng công thức ![]()
y' = 3(x2 – x + 1)2(x2 – x + 1)’(x2 + x + 1) + 2(x2 + x + 1)(x2 + x + 1)’(x2 – x + 1)3
y’ = 3(x2 – x + 1)2(2x – 1)(x2 + x + 1)2 + 2(x2 + x + 1)(2x + 1)(x2 – x + 1)3
y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)].
Tính đạo hàm của hàm số y = ( x 2 – x + 1 ) 1 3
A. y ' = 2 x - 1 3 x 2 - x + 1 3
B. y ' = 2 x - 1 3 x 2 - x + 1 2 3
C. y ' = 2 x - 1 x 2 - x + 1 2 3
D. y ' = 1 3 x 2 - x + 1 2 3
Tính đạo hàm của hàm số y = ( x - 2 ) x 2 + 1
A. y ' = 2 x 2 - 2 x - 1 x 2 + 1
B. y ' = 2 x 2 + 2 x + 1 x 2 + 1
C. y ' = 2 x 2 - 2 x + 1 x 2 - 1
D. y ' = 2 x 2 - 2 x + 1 x 2 + 1
Tính đạo hàm của hàm số y = ln ( x + x 2 + 1 )
A. y ' = 1 x + x 2 + 1
B. y ' = 1 x 2 + 1
C. y ' = x + x 2 + 1
d. y ' = x x + x 2 + 1
Tính đạo hàm của hàm số y = ln ( x 2 + 1 - x )
A. y ' = - 1 x 2 + 1 - x
B. y ' = - 1 x 2 + 1
C. y ' = 1 x 2 + 1
D. y ' = x x 2 + 1
Tính đạo hàm của hàm số sau y = x 2 - x + 1 x - 1
A. x 2 - 2 x x - 1 2
B. x 2 + 2 x x - 1 2
C. x 2 + 2 x x + 1 2
D. - 2 x - 2 x - 1 2
Chọn A
y ' = ( 2 x − 1 ) . ( x − 1 ) − 1. ( x 2 − x + 1 ) ( x − 1 ) 2 = 2 x 2 − 2 x − x + 1 − x 2 + x − 1 ( x − 1 ) 2 = x 2 − 2 x ( x − 1 ) 2
Tính đạo hàm của hàm số y = x 2 − x + 1 3 tại điểm x = − 1 .
A. 27
B. -27
C. 81
D. -81
Đáp án D
Ta có y ' = 3 x 2 − x + 1 2 2 x − 1 ⇒ y − 1 = − 81
Tính đạo hàm của các hàm số sau: y = 1 + x - x 2 1 - x + x 2
Đạo hàm của hàm số
y = ( x 2 + x + 1 ) 1 / 3