Tìm a,b để hàm số sau có đạo hàm trên R
f(x)= x 2 - x + 1 khi x ≤ 1 - x 2 + ax + b khi x > 1
A. a=3; b=-1
B. a=3; b=-11
C. a=13;b=-1
D. a=23; b=-21
Tìm a, b để các hàm số sau có đạo hàm trên R: f ( x ) = x 2 - x + 1 k h i x ≤ 1 - x 2 + a x + b k h i x > 1
A. a = 13 b = - 1
B. a = 3 b = - 11
C. a = 23 b = - 21
D. a = 3 b = - 1
- Với x ≠ 1 thì hàm số luôn có đạo hàm.
- Do đó hàm số có đạo hàm trên R khi và chỉ khi hàm số có đạo hàm tại x=1.
- Ta có:
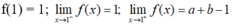
→ Hàm số liên tục trên R
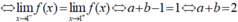
- Khi đó:
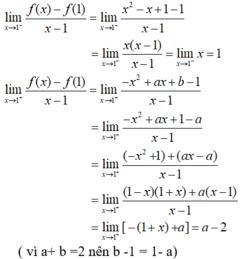
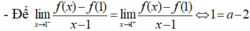
- Nên hàm số có đạo hàm trên R thì:
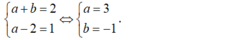
Chọn D
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]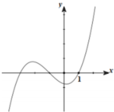
![]()
![]()
![]()
![]()
Tìm a; b để các hàm số sau có đạo hàm trên R. f x = x 2 - x + 1 k h i x ≤ 1 - x 2 + a x + b k h i x > 1
A. a = 13 b = - 1
B. a = 3 b = - 11
C. a = 23 b = - 21
D. a = 3 b = - 1
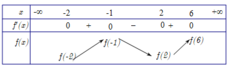
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = x 2 ( x - 2 ) ( x 2 - 6 x + m ) , với mọi x ∈ R . Có bao nhiêu số nguyên m thuộc đoạn - 2019 ; 2019 để hàm số g ( x ) = f ( 1 - x ) nghịch biến trên khoảng - ∞ ; - 1
A. 2012
B. 2011
C. 2009
D. 2010
Cho hàm số y= f(x) có đạo hàm f'(x) liên tục trên R và đồ thị của hàm số f'(x) trên đoạn [ -2;6] như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau.
A. maxf x − 2 ; 6 = f − 1
B. maxf x − 2 ; 6 = f − 2
C. maxf x − 2 ; 6 = f 6
D. maxf x − 2 ; 6 = m ax f − 1 , f 6
Đáp án là D
Đồ thị f ' x có bảng biến thiên:
max [ − 2 ; 6 ] f ( x ) = max { f ( − 1 ) , f ( 6 ) } .