Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
Tính giá trị của của P   1 + i 1 - i 4   +   1 - i 1 + i...
Đọc tiếp
Lớp 12 Toán
Những câu hỏi liên quan
Ngọc Duyên DJ
1/ Tìm giá trị nhỏ nhất của biểu thức B 2I3x-6I - 4 2/ Tìm x thuộc Z để biểu thức D I x-2 I + I x-8 I đạt Gía trị nhỏ nhất3/ Tìm GTNN của biểu thức B I x-2017 I + I x-1 I                                         A I x-2017 I + I x-2 I4/ với giá trị nào của x,y thì biểu thức C I x-100 I + I y+20 I - 1 có giá trị nhỏ nhất . Tìm GTNN5/ Với giá trị nào của x thì biểu thức A 100 - I x+5 I có giá trị lớn nhất. Tính GTLN đógiúp với ạ ._.
Đọc tiếp
Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
Huy Hoàng
Huy Hoàng
18 tháng 12 2017 lúc 12:48

1/ Gọi Bmin là GTNN của B

Ta có \(\left|3x-6\right|\ge0\)=> \(2\left|3x-6\right|\ge0\)với mọi \(x\in R\)

=> \(2\left|3x-6\right|-4\ge0\)với mọi \(x\in R\).

=> Bmin = 0.

Vậy GTNN của B = 0.

2/ Gọi Dmin là GTNN của D.

Ta có \(\left|x-2\right|\ge0\)với mọi \(x\in R\)

và \(\left|x-8\right|\ge0\)với mọi \(x\in R\)

=> \(\left|x-2\right|+\left|x-8\right|\ge0\)với mọi \(x\in R\)

=> Dmin = 0.

=> \(\left|x-2\right|+\left|x-8\right|=0\)

=> \(\hept{\begin{cases}\left|x-2\right|=0\\\left|x-8\right|=0\end{cases}}\)=> \(\hept{\begin{cases}x-2=0\\x-8=0\end{cases}}\)=> \(\hept{\begin{cases}x=2\\x=8\end{cases}}\)(Vô lý! Không thể cùng lúc có 2 giá trị x xảy ra)

Vậy không có x thoả mãn đk khi GTNN của D = 3.

Bình luận (0)
Pham Trong Bach
Cho biết I ∫ 0 π 2 x sin x + 2 m d x 1 + π 2 . Tính giá trị của m - 1 A. 4 B. 2 C. 3 D. 5
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
3 tháng 1 2019 lúc 10:11

Sử dụng phương pháp tích phân từng phần (hoặc bấm máy tính) ta có được ∫ 0 π 2 x sin x d x = 1

Khi đó 

I = 1 + 2 m ∫ 0 π 2 x d x = 1 + m π 2 4 = 1 + π 2 ⇒ m = 4 ⇒ m - 1 = 3

Đáp án C

Bình luận (0)
Ngọc Duyên DJ

3/ Tìm GTNN của biểu thức B = I x-2017 I + I x-1 I

                                         A= I x-2017 I + I x-2 I

4/ với giá trị nào của x,y thì biểu thức C = I x-100 I + I y+20 I - 1 có giá trị nhỏ nhất . Tìm GTNN

5/ Với giá trị nào của x thì biểu thức A= 100 - I x+5 I có giá trị lớn nhất. Tính GTLN đó

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
Nguyễn Thái Sơn
Nguyễn Thái Sơn
22 tháng 3 2020 lúc 21:49

Tìm GTNN của biểu thức B = I x-2017 I + I x-1 I

có  |x-2017|luôn\(\ge0\forall x\in Q\)

cũng có |-1|luôn\(\ge0\forall x\in Q\)

=>I x-2017 I + I x-1 I\(\ge0\forall x\in Q\)

=> I x-2017 I + I x-1 I=|x-2017|+|1-x|=|x-2017+1-x|=2016

dấu''='' xảy ra <=>(x-2017)(1-x)=0

TH1:

=>\(\orbr{\begin{cases}x-2017\ge0\\1-x\le0\end{cases}}\)

TH2: 

=> \(\orbr{\begin{cases}x-2017\le0\\1-x\ge0\end{cases}}\)

tự làm típ ! xét 2 TH thấy cái nào mà nó vô lí thì đánh vô lí chọn TH còn lại nhé !

 
Bình luận (0)
Khách vãng lai đã xóa
Pham Trong Bach
Cho số phức z thỏa mãn | ( z + 2 ) i + 1 | + | ( z ¯ - 2 ) i - 1 | 10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng SM+m.
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
24 tháng 4 2018 lúc 14:21

Đáp án C.

Bình luận (0)
Đào Minh Hiếu

I= tuyệt đối của x+1 + tuyệt đối của x+4 +tuyệt đối của x+3

Tính Giá trị nhỏ nhất của I và với x =bao nhiêu

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
l҉o҉n҉g҉ d҉z҉
l҉o҉n҉g҉ d҉z҉
30 tháng 9 2020 lúc 20:51

I = | x + 1 | + | x + 4 | + | x + 3 |

= | x + 3 | + ( | x + 1 | + | x + 4 | )

Ta có :

+) | x + 3 | ≥ 0 ∀ x (1)

+) | x + 1 | + | x + 4 |

= | x + 1 | + | -( x + 4 ) |

= | x + 1 | + | -x - 4 | ≥ | x + 1 - x - 4 | = | -3 | = 3 (2)

Cộng (1) với (2) theo vế

=> | x + 3 | + ( | x + 1 | + | x + 4 | ) ≥ 3 ∀ x

Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left|x+3\right|=0\\\left(x+1\right)\left(-x-4\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\-4\le x\le-1\end{cases}}\Leftrightarrow x=-3\)

=> MinI = 3 <=> x = -3

Bình luận (0)
Khách vãng lai đã xóa
Pham Trong Bach
Cho số phức z thỏa mãn điều kiện z - 1 - 2 i 4  Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z + 2 + i  Tính giá trị của tổng SM2+ m2  A. S 82 B. . S 34 C. S 68 D. S 36.
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
2 tháng 4 2019 lúc 12:42

Chọn C

Bình luận (0)
Pham Trong Bach
Cho số thực z 1  và số phức z 2  thỏa mãn z 2 - 2 i 1  và z 2 - z 1 1 +...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
4 tháng 3 2018 lúc 4:37

Bình luận (0)
Pham Trong Bach
Cho các số phức z 1 1 , z 2 2 − 3 i  và các số z thỏa mãn z − 1 − i + z − 3 + i 2 2 ....
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
14 tháng 8 2017 lúc 16:41

Bình luận (0)
Pham Trong Bach
Xét các số phức z thỏa mãn thiết | z + 2 - i| + | z - 4 - 7i| 6 2  . Gọi m, M  lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z – 1 + i|. Tính  P m + M.
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
19 tháng 7 2017 lúc 5:45

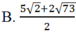
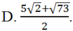
Chọn B.

Ta có: 

Suy ra: 

Xét điểm A(-2; 1) và  B(4; 7) , phương trình đường thẳng  AB: x - y + 3 = 0.

Gọi M(x; y)  là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Khi đó ta có  và ta thấy , suy ra quỹ tích M  thuộc đoạn thẳng AB.

Xét điểm C( 1; -1); ta có  , hình chiếu H  của C trên đường thẳng AB nằm trên đoạn AB.

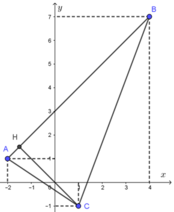
Do đó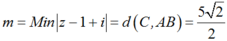 

Vậy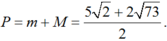 

Bình luận (0)
Trinhdiem

a) Rút gọn A và tìm điều kiện của x để giá trị của A được xác định. b) Tính giá trị của A tại x = -2. c) Tính giá trị của x để giá trị của A = 4. d) Tính giá trị của x để giá trị của A = 1

Xem chi tiết
Lớp 8 Toán

Khách
 
Thảo Thảo
Thảo Thảo
26 tháng 12 2021 lúc 20:41

a) ĐKXĐ: x≠ \(\dfrac{1}{2}\); x≠ \(\dfrac{-1}{2}\); x≠0

    A= \(\left(\dfrac{1}{2x-1}+\dfrac{3}{1-4x^2}-\dfrac{2}{2x+1}\right):\dfrac{x^2}{2x^2+x}\)

       = \(\left(\dfrac{2x+1-3-2\left(2x-1\right)}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)

       =  \(\left(\dfrac{2x+1-3-4x+2}{4x^2-1}\right):\dfrac{x^2}{2x^2+x}\)

       = \(\dfrac{-4x}{\left(2x+1\right)\left(2x-1\right)}.\dfrac{x\left(2x+1\right)}{x^2}\)

       =  \(\dfrac{-4x^2}{x^2\left(2x-1\right)}\)

       = \(\dfrac{-4}{2x-1}\)

b) Tại x= -2 ta có A= \(\dfrac{-4}{2.\left(-2\right)-1}\)= \(\dfrac{4}{5}\)

c)  A= 4 ta có \(\dfrac{-4}{2x-1}\)=4

                  ⇔ -4 = 4(2x-1)

                  ⇔ -4 = 8x-4 

                   ⇔ x = 0

d)  A=1 ta có \(\dfrac{-4}{2x-1}\)=1

                   ⇔  -4 = 2x-1

                    ⇔ x= \(\dfrac{-3}{2}\)

Bình luận (0)