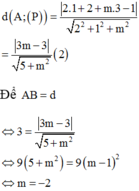Trong không gian tọa độ Oxyz, tìm tất cả các giá trị của tham số m đường thẳng d : x - 2 - 2 = y + 2 1 = z - 1 1 song song với mặt phẳng P : 2 x + 1 - 2 m y + m 2 z + 1 = 0 .
A. m ∈ - 1 ; 3
B. m = 3
C. m = -1
D. Không có giá trị nào của m.
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Trong không gian tọa độ Oxyz cho đường thẳng d : x = - 1 + t y = 1 + t z = 1 - t , t ∈ R và mặt phẳng α : m 2 x - 3 y + z + 3 m = 0 (với m là tham số). Tìm tất cả giá trị của tham số m để đường thẳng d song song với mặt phẳng α
A. -2
B. 2 hoặc -2
C. 2
D. 1 hoặc 2
Trong không gian với hệ trục tọa độ Oxyz, tìm tất cả giá trị thực của tham số m để đường thẳng d : x - 2 - 2 = y - 1 1 = z 1 song song với mặt phẳng P : 2 x + 1 - 2 m y + m 2 z + 1 = 0 .
A. m ∈ - 1 ; 3
B. m=3
C. Không có giá trị nào của m
D. m=-1
Trong không gian với hệ trục tọa độ Oxyz, cho A(1;0;−1),B(2;1;0). Tìm tất cả các giá trị thực của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng x + y + mz − 3 = 0 bằng độ dài đoạn thẳng AB.
A. m = ± 1
B. m = 1
C. m = ± 2
D. m = 2
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d 1 : x + 1 2 = 1 - y - m = 2 - z - 3 và d 2 : x - 3 1 = y 1 = z - 1 1 . Tìm tất cả các giá trị thực của m để d 1 ⊥ d 2 được:
A. -1
B. 1
C. -5
D. 5
Trong không gian với hệ trục tọa độ Oxyz, cho A 1 ; 2 ; 3 , B 3 ; 4 ; 4 . Tìm tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng 2 x + y + m z − 1 = 0 bằng độ dài đoạn thẳng AB.
A. m = 2
B. m = -2
C. m = -3
C. m = ± 2
Đáp án A
A B → = 2 ; 2 ; 1 ⇒ A B = 3
Khoảng cách từ A đến mặt phẳng α : 2 x + y + m z − 1 = 0 bằng AB nên
d A ; α = 2 x A + y A + m z A − 1 2 2 + 1 2 + m 2 = A B = 3 ⇔ 3 m + 3 m 2 + 5 = 3 ⇔ 3 m + 1 = 3 m 2 + 5 ⇔ m + 1 2 = m 2 + 5 ⇔ m = 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y + 2 2 + z 2 = 5 . Tìm tất cả các giá trị thực của tham số m để đường thẳng ∆ : x - 1 2 = y + m 1 = z - 2 m - 3 cắt (S) tại hai điểm phân biệt A, B sao cho A, B có độ dài AB lớn nhất.
A. m = - 1 2
B. m = ± 1 3
C. m = 1 2
D. m = 0
Đáp án D
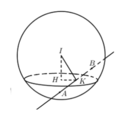
Phương pháp: AB lớn nhất
![]()
Cách giải: Mặt cầu (S) có tâm I(0;-2;0) và bán kính R = 5
![]()
Ta có
![]()
![]()
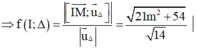
Để AB lớn nhất
![]()
Trong không gian với hệ tọa độ Oxyz, cho O A → = 3 i → + j → − 2 k → v à B m ; m − 1 ; − 4 . Tìm tất cả các giá trị của tham số m để độ dài đoạn AB = 3.
A. m = 3 hoặc m = 4
B. m = 2 hoặc m = 3
C. m = 1 hoặc m = 2
D. m = 1 hoặc m = 4
Trong không gian với hệ trục tọa độ Oxyz, cho A(1;2;3), B(3;4;4). Tìm tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng 2 x + y + m z - 1 = 0 bằng độ dài đoạn thẳng AB.
A. m = 2
B. m = -2
C. m = -3
D. m = ± 2
Đáp án B.
Ta có:
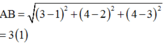
Khoảng cách từ A dến mặt phẳng (P):
![]()