Xét các trường hợp:

\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương 

\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương

\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương 

\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương

Vậy \(n\in\left\{1;3\right\}\).

Đáp án B.

Ta có u n = u n − 1 + n − 1 3 ⇔ u n − u n − 1 = n − 1 3 ⇒ u n − 1 − u n − 2 = n − 2 3 .

Tương tự, ta được u 2 − u 1 = 1 3 .  Cộng trừ 2 vế suy ra u n − u 1 = 1 3 + 2 3 + ... + n − 1 3  

⇔ u n − 1 = n n − 1 2 2 ⇒ u n − 1 = n n − 1 2 ≥ 2039190 ⇔ n ≥ 2020.

Đáp án A

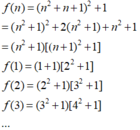
= > U n = ( 1 2 + 1 ) ( 2 2 + 1 ) . ( 3 2 + 1 ) ( 4 2 + 1 ) ... [ ( 2 n − 1 ) 2 + 1 ] [ ( 2 n ) 2 + 1 ] ( 2 2 + 1 ) ( 3 2 + 1 ) . ( 4 2 + 1 ) ( 5 2 + 1 ) ... [( 2 n ) 2 + 1 ] [ ( 2 n + 1 ) 2 + 1 ] = > U n = 2 ( 2 n + 1 ) 2 + 1

Đáp án là A

a/ \(10^n+2^3=1000...08\) (n-1 chữ số 0)

Tổng các chữ số của \(10^n+2^3\) là \(1+8=9⋮9\Rightarrow10^n+2^3⋮9\)

b/ \(10^n+26=1000...026\) (n-2 chữ số 0)

\(1000...026⋮2\Rightarrow10^n+26⋮2\)

Tổng các chữ số của \(10^n+26\) là \(1+2+6=9⋮9\Rightarrow10^n+26⋮9\)

Mà 2 và 9 là 2 số nguyên tố cùng nhau

\(\Rightarrow10^n+26⋮2.9=18\)

c/

\(9^{2n+1}=9.9^{2n}\)

\(9^{2n}=\left(9^2\right)^n=81^n\) có chữ số hàng đơn vị là 1

\(\Rightarrow9^{2n+1}=9.9^{2n}\) có chữ số hàng đơn vị là 9

\(\Rightarrow9^{2n+1}+1\) có chữ số hàng đơn vị là 0 \(\Rightarrow9^{2n+1}+1⋮10\)

Đáp án là B

Đáp án là B

xời dăm ba cái bài này tui...........................ko thik làm 

+ Ta có: \(6n⋮6\forall n\)\(\Rightarrow\)\(6n+3:6\)dư  \(3\)

                                            \(6n-3:6\)dư  \(6-3=3\)

+ Ta lại có: \(6.\left(n+3\right)⋮6\forall n\)\(\Rightarrow\)\(6.\left(n+3\right)+3:6\)dư  \(3\)

Vậy \(6n+3,\)\(6n-3,\)\(6.\left(n+3\right)+3\)chia 6 dư 3

6.n + 3               (với n ∈ ℕ)  ( vì \(6n⋮6\), 3 không chia hết cho 6 )

6.n - 3                (với n ∈ ℕ )   (  vì \(6n⋮6\), 3 không chia hết cho 6  )

6.(n + 3) + 3       (với n ∈ ℕ)  ( vì \(6\left(n+3\right)⋮6\), 3 không chia hết cho 6 )

\(\rightarrow\)Chia 6 dư 3