Cho hàm số y=sin2x.Hãy chọn khẳng định đúng .
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số: y = lnx x Chọn khẳng định đúng.
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có một cực đại và một cực tiểu
Cho hàm số y=f(x) liên tục và có đạo hàm tới cấp hai trên a,b ; x 0 ∈ a ; b . Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu f ' x 0 = 0 f ' ' x 0 < 0 thì x 0 là một điểm cực tiểu của hàm số
B. Nếu f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x 0 là một điểm cực trị của hàm số.
C. Nếu f ' x 0 = 0 f ' ' x 0 > 0 thì x 0 là một điểm cực đại của hàm số
D. A, B, C đều sai.
Cho hàm số y = f ( x ) c ó f ' ( x ) > 0 , ∀ x ∈ ( a , b ) Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số đồng biến trên ( a , b )
B. Hàm số nghịch biến trên ( a , b )
C. Hàm số nhận giá trị không đổi trên ( a , b )
D. Hàm số đồng biến trên ℝ
Cho hàm số y = a x 3 + b x 2 + c x + d a ≠ 0 có đồ thị như hình vẽ. Chọn khẳng định đúng?
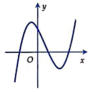
A. a > 0, d > 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0, d > 0.
D. a > 0, c < 0, d > 0.
Đáp án D
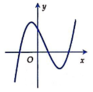
+ Có a>0
+ y 0 = d ⇒ d > 0 (giao với Oy – hoành độ giao điểm)
+ y ' = 3 a x 2 + 2 b x + c ⇒ Δ > 0 ⇒ b 2 > 3 a c
Nghiệm y ' = 0 là x 1 , x 2 ⇒ x 1 . x 2 = c 3 a < 0 ⇒ c < 0
Cho hàm số y = a x 3 + b x 2 + c x + d a ≠ 0 có đồ thị như hình vẽ. Chọn khẳng định đúng?
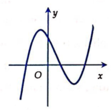
A. a > 0 , d > 0.
B. a > 0 , b < 0 , c > 0.
C. a > 0 , b > 0 , c > 0 , d > 0.
D. a > 0 , c < 0 , d > 0.
Cho hàm số y=x^3+3x+m, với m là tham số thực . Biết giá trị lớn nhất của hàm số trên [0,1]=4. Chọn khẳng định đúng a)m thuộc (2,6) b) m thuộc (-5,0) c) m thuộc (-2,2) d) m thuộc (6,10)
Cho hàm số: 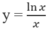 Chọn khẳng định đúng.
Chọn khẳng định đúng.
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có một cực đại và một cực tiểu
Đáp án : B.
Hướng dẫn: Tính đạo hàm và lập bảng biến thiên.
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị hình dưới :
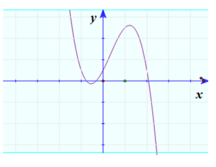
Chọn khẳng định đúng.
A. a<0 ; b<0 ; c>0 ; d>0
B. a<0 ; b>0 ; c>0 ; d>0
C. a<0 ; b>0 ; c<0 ; d<0
D. a>0 ; b>0 ; c>0 ; d>0
Đáp án B

Nhánh cuối của đồ thị đi xuông a < 0
Tích hai điểm cực trị của hàm số là số âm ⇒ a , c trái dấu c > 0
Tổng hai điểm cực trị của hàm số là số dương ⇒ a , b trái dấu ⇒ b > 0
Cho hàm số y = a x 3 + b x 2 + c x + d , a , b , c , d ∈ ℝ có đồ thị như dưới đây. Tìm khẳng định đúng trong các khẳng định sau?
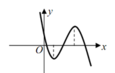
A. a < 0, b < 0, c < 0, d > 0, b 2 > 3 a c
B. a < 0, b < 0, c > 0, d > 0, b 2 > 3 a c
C. a < 0, b > 0, c < 0, d > 0, b 2 > 3 a c
D. a < 0, b > 0, c > 0, d > 0, b 2 > 3 a c
Đáp án C
Từ đồ thị hàm số ta suy ra a<0. Để ý rằng đồ thị hàm số giao với Ox tại 3 điểm có hoành độ dương và hai cực trị nằm về hai phía của trục tung. Giải hệ điều kiện đó ta thu được các giá trị a < 0, b > 0, c < 0, và d > 0.
Chọn phương án C.