Trong bốn giới hạn sau đây, giới hạn nào có kết quả bằng
+
∞
?
Đọc tiếp
Trong bốn giới hạn sau đây, giới hạn nào có kết quả bằng + ∞ ?
Những câu hỏi liên quan
Trong các giới hạn sau đây giới hạn nào có kết quả bằng +∞. A.
lim
x
→
0
1
x
B.
lim
x
→
1
+
1
-
x
+
1
C.
lim...
Đọc tiếp
Trong các giới hạn sau đây giới hạn nào có kết quả bằng +∞.
A. lim x → 0 1 x
B. lim x → 1 + 1 - x + 1
C. lim x → - ∞ x 2 + x - x
D. lim x → + ∞ x 2 + x + 1 - x + 1
Trong các giới hạn sau đây, giới hạn nào có kết quả bằng 1? A.
l
i
m
3
n
+
1
+
2
n
3
n
+
5
B.
l
i
m
3...
Đọc tiếp
Trong các giới hạn sau đây, giới hạn nào có kết quả bằng 1?
A. l i m 3 n + 1 + 2 n 3 n + 5
B. l i m 3 n 2 + n 4 n 2 - 5
C. l i m 2 n 3 + 3 2 n 2 + 1
D. l i m n 2 + 2 n - n 2 - 1
Trong bốn giới hạn sau đây, giới hạn nào có giá trị bằng 0 ? A.
lim
2
n
+
3
1
−
2
n
B.
lim
2
n...
Đọc tiếp
Trong bốn giới hạn sau đây, giới hạn nào có giá trị bằng 0 ?
A. lim 2 n + 3 1 − 2 n
B. lim 2 n + 1 n − 3 2 n − 2 n 3
C. lim 2 n + 1 3.2 n − 3 n
D. lim 1 − n 3 n 2 + 2 n
Đáp án C
Ta có: lim 2 n + 1 3.2 n − 3 n = lim 2 n 1 + 1 2 n 3 n . 3. 2 3 n − 1 = lim 2 3 n . lim 1 + 1 2 n 3. 2 3 n − 1 = 0. − 1 = 0
Nhận xét: Ta có thể chọn nhanh đáp án như sau: giói hạn lũy thừa ở phương án C có cơ số lớn nhất trên tử nhỏ hơn cơ số lớn nhất dưới mẫu nên giới hạn tiến về 0.
Đúng 0
Bình luận (0)
Trong bốn giới hạn sau đây, giới hạn nào bằng
−
∞
? A.
lim
x
→
−
∞
−
3
x
+
4
x
−
2
B.
lim
x...
Đọc tiếp
Trong bốn giới hạn sau đây, giới hạn nào bằng − ∞ ?
A. lim x → − ∞ − 3 x + 4 x − 2
B. lim x → + ∞ − 3 x + 4 x − 2
C. lim x → 2 + − 3 x + 4 x − 2
D. lim x → 2 + − 3 x + 4 x − 2
Đáp án C
Ta có lim x → 2 + − 3 x + 4 = − 2 < 0 và lim x → 2 + x − 2 = 0 x − 2 > 0 ∀ x . Vậy lim x → 2 + − 3 x + 4 x − 2 = − ∞
Nhận xét: Ta có thể chọn nhanh đáp án bằng cách loại ngay 2 phương án A và B do bậc tử bằng bậc mẫu nên giới hạn luôn hữu hạn khi x → ∞ . Ở phương án C thì khi trên tử âm còn mẫu dương nên giới hạn tiến về − ∞ .
Đúng 0
Bình luận (0)
Trong bốn giới hạn sau đây, giới hạn nào bằng - ∞ ?
Trong bốn giới hạn sau đây, giới hạn nào bằng
-
∞
? A. B. C. D.
Đọc tiếp
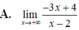
Trong bốn giới hạn sau đây, giới hạn nào bằng - ∞ ?
A.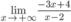
B.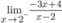
C.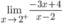
D.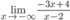
Giới hạn nào sau đây có kết quả bằng 0. A.
l
i
m
n
2
+
n
n
2
+
10
n
B.
l
i
m
2
n
+
700
n...
Đọc tiếp
Giới hạn nào sau đây có kết quả bằng 0.
A. l i m n 2 + n n 2 + 10 n
B. l i m 2 n + 700 n 3 + 1
C. l i m 10 - 3 n
D. l i m 1 - n n 2 + 10 n
Trong các giới hạn sau, giới hạn nào có kết quả là 0? A.
l
i
m
x
→
1
x
-
1
x
3
-
1
B.
l...
Đọc tiếp
Trong các giới hạn sau, giới hạn nào có kết quả là 0?
A. l i m x → 1 x - 1 x 3 - 1
B. l i m x → - 2 2 x + 5 x + 10
C. l i m x → 1 x 2 - 1 x 2 - 3 x + 2
D. l i m x → + ∞ x 2 + 1 - x
Trong các giới hạn sau, giới hạn nào có kết quả là 0 A.
lim
x
→
1
x
-
1
x
3
-
1
B.
lim
x
→
-...
Đọc tiếp
Trong các giới hạn sau, giới hạn nào có kết quả là 0
A. lim x → 1 x - 1 x 3 - 1
B. lim x → - 2 2 x + 5 x + 10
C. lim x → 1 x 2 - 1 x 2 - 3 x + 2
D. lim x → + ∞ ( x 2 + 1 - x )
