Tìm tất cả các giá trị thực của tham số a sao cho hai đường thẳng sau đây cắt nhau.
d : x = 1 + a 2 t y = t z = - 1 + 2 t ⇔ t ∈ ℝ và d ' : x = 3 - t ' y = 2 + t ' z = 3 - t t ' ∈ ℝ
A. a ∈ ℝ
B. a = - 1
C. a = 1
D. a = ± 1
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số a sao cho hai đường thẳng sau đây cắt nhau.
d
:
x
1
+
a
2
t
y
t
z...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a sao cho hai đường thẳng sau đây cắt nhau. d : x = 1 + a 2 t y = t z = − 1 + 2 t t ∈ ℝ và d ' : x = 3 − t ' y = 2 + t ' z = 3 − t ' t ' ∈ ℝ
A. a ∈ ℝ
B. a=-1
C. a=1
D. a = ± 1
Đáp án D.
Hai đường thẳng d và d ' cắt nhau khi và chỉ khi hệ phương trình
1 + a 2 t = 3 − t ' t = 2 + t ' − 1 + 2 t = 3 − t ' có đúng một nghiệm ⇔ t = 2 t ' = 0 a = ± 1 .
Vậy ta chọn D.
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
-
1
x
-
1
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB 4 A. m -1 B.
[
m
0...
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4
A. m = -1
B. [ m = 0 m = 3
C. [ m = - 1 m = 3
D. m = 4
Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
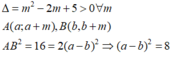
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
+
1
x
+
1
có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn
A
B
2
3
A.
m
2
±
10...
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 10
C. m = 4 ± 3
D. m = 2 ± 3
Xét phương trình hoành độ giao điểm:
2 x + 1 x + 1 = x + m - 1 ( x ≠ - 1 ) ⇔ x 2 + ( m - 2 ) x + ( m - 2 ) = 0 ( * )
Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt khác - 1
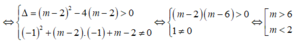
Khi đó d cắt ( C) tại A( x1; x1+ m- 1) ; B ( x2; x2+ m- 1)
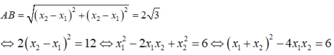
Áp dụng định lý Vi-et x 1 + x 2 = - m + 2 x 1 x 2 = m - 2 ta có:
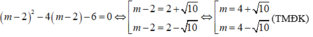
Vậy m = 4 ± 10
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
−
1
x
−
1
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng
d
:
y
x
+
m
cắt (C) tại hai điểm phân biệt A, B sao cho AB 4 A.
m...
Đọc tiếp
Cho hàm số y = 2 x − 1 x − 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4
A. m = − 1.
B. m = 0 m = 3 .
C. m = − 1 m = 3 .
D. m = 4.
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình
x
6
+
t
y
-
2
-
5
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Đúng 0
Bình luận (0)
Cho hàm số
C
:
y
x
x
-
1
và đường thẳng
d
:
y
x
+
m
.
Tập tất cả các giá trị của tham số m sao cho (C) và d cắt nhau tại hai điểm phân biệt là A. (-2;2) B.
-
∞
;...
Đọc tiếp
Cho hàm số C : y = x x - 1 và đường thẳng d : y = x + m . Tập tất cả các giá trị của tham số m sao cho (C) và d cắt nhau tại hai điểm phân biệt là
A. (-2;2)
B. - ∞ ; - 2 ∪ 2 ; + ∞
C. R
D. ∅
Chọn C.
Phương trình hoành độ giao điểm của đồ thị (c) và đường thẳng d:
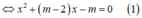
(C) cắt d tại hai điểm phân biệt ⇔(1) có hai nghiệm phân biệt
Vậy d luôn cắt (C) tại 2 điểm phân biệt.
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
+
1
x
+
1
có đồ thị (C). Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng
d
:
y
x
+
m
−
1
cắt (C) tại hai điểm phân biệt ABthỏa mãn
A
B
2
3
A....
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d : y = x + m − 1 cắt (C) tại hai điểm phân biệt ABthỏa mãn A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 10
C. m = 4 ± 3
D. m = 2 ± 3
Đáp án B
Phương pháp: Xét phương trình hoành độ giao điểm, đưa phương trình về phương trình bậc hai và sử dụng công thức tính khoảng cách, định lý Vi-et cho phương trình bậc hai để tìm m
Cách giải:
Xét phương trình hoành độ
giao điểm:
Vậy m = 4 ± 10
Đúng 0
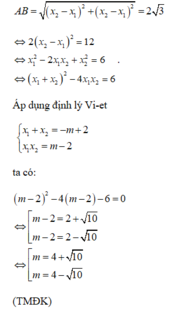
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị (C) của hàm số
y
2
x
+
3
x
-
1
cắt đường thẳng
△
:
y
x
+
m
tại hai điểm phân biệt A và B sao cho tam giác OAB vuông tại O A.
m
-
3
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị (C) của hàm số y = 2 x + 3 x - 1 cắt đường thẳng △ : y = x + m tại hai điểm phân biệt A và B sao cho tam giác OAB vuông tại O
A. m = - 3
B. m = 6
C. m = 5
D. m = - 1
Cho hàm số y
2
x
-
1
x
-
1
có đồ thị ( c ).Tìm tất cảc các giá trị thực của tham số m để đường thẳng: d: y x +m và cắt ( c ) tại hai điểm phân biệt A, B sao cho AB 4. A. m -1 B. C. D. m4
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị ( c ).Tìm tất cảc các giá trị thực của tham số m để đường thẳng: d: y= x +m và cắt ( c ) tại hai điểm phân biệt A, B sao cho AB = 4.
A. m= -1
B.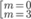 
C.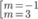 
D. m=4
