Cho dãy số u n thỏa mãn ln 2 u 6 - ln u 6 = ln u 4 - 1 và u n + 1 = u n . e với mọi n ≥ 1 . Tìm u 1
A. e
B. e 2
C. e - 3
D. e - 4
Cho dãy số (un) thỏa mãn ln2u6 – ln u6 = ln u4 – 1 và un+1 = un.e với mọi n ≥ 1 Tìm u1
A. e
B. e2
C. e-3
D. e-4
Chọn D.
Vì un+1 = un.e nên dễ thấy dãy số (un) là cấp số nhân có công bội q = e
ln2u6 – (ln u8 +ln u4) + 1 = 0 ⇔ ln2u6 – (ln u8u4) + 1 = 0 ⇔ (ln u6 – 1)2 = 0
⇔ ln u6 = 1 ⇔ u6 = e ⇔ u1 = e-4
Cho dãy số ( u n ) thoả mãn u n = u n - 1 + l n ( n + 1 n ) , ∀ n ≥ 2 và u 1 = 2 . Tìm số tự nhiên n nhỏ nhất để u n > 10 .
A. 5962.
B. 5960.
C. 5963.
D. 5961.
Cho x,y là các số thực dương thỏa mãn ln x + ln y ≥ ln x 2 + y Tìm giá trị nhỏ nhất của P=x+y
A. 6
![]()
![]()
![]()
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln x 2 + y . Tính giá trị nhỏ nhất của P = x + y.
![]()
![]()
![]()
![]()
Đáp án B
Ta có ln x y = ln x + ln y ≥ ln x 2 + y
⇔ x y ≥ x 2 + y ⇔ y x - 1 ≥ x 2
Vì x = 1 không thỏa và y > 0 => x > 1
⇒ P = x y ≥ x 2 x - 1 + x = f x
X é t h à m s ố f x = x 2 x - 1 + x v ớ i x > 1
⇒ f ' x = x 2 - 2 x x - 1 2 + x = 2 x 2 - 4 x + 1 x - 1 2
⇒ f ' x = 0 ⇔ x = 2 + 2 2 v ì x > 1
Dựa vào bảng biến thiên của hàm số f(x) suy ra
⇒ M i n P = M i n x > 1 f x = f 1 = 3 + 2 2 .
Cho số thực dương k > 0 thỏa mãn ∫ 0 2 d x x 2 + k = ln ( 2 + 5 ) . Mệnh đề nào sau đây đúng?
![]()
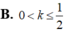
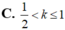
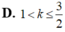
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P = x + y
A. P = 6
B. P = 2 + 3 2
C. P = 3 + 2 2
D. P = 17 + 3
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln ( x 2 + y ) là các số thực dương thỏa mãn P = x + y
![]()
![]()
![]()
![]()
Giá trị x thỏa mãn 2 x - 2 = ln 2 thuộc
A. ( 0 ; 3 2 )
B. ( 3 2 ; 2 )
C. ( 3 4 ; 1 )
D. ( 5 3 ; 2 )
Cho x y, là các số thực dương thỏa mãn l n x + l n y ≥ l n ( x 2 + y ) . Tìm giá trị nhỏ nhất của
A. P = 6
B. P = 3 + 2 2
C. P = 2 + 3 2
D. P = 17 + 3
Cho hàm số f(x) liên tục trên ℝ thỏa mãn ∫ 0 99 f ( x ) d x = 2 . Khi đó tích phân I = ∫ 0 e 99 - 1 x x 2 + 1 f ( ln ( x 2 + 1 ) ) d x bằng bao nhiêu?
A. 1.
B. 2.
C. 3.
D. 4.