Cho phương trình: x2 - x - 2 = 0.
Vẽ hai đồ thị y = x2 và y = x + 2 trên cùng một hệ trục tọa độ
Cho phương trình: x 2 - x - 2 = 0 .
a) Giải phương trình.
b) Vẽ hai đồ thị y = x 2 và y = x + 2 trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
a) x 2 – x – 2 = 0
Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.
Vậy tập nghiệm của phương trình là S = {-1; 2}
b) + Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).
+ Parabol y = x 2 đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).
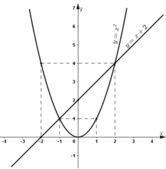
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
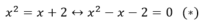
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị
Bài 3:a)Trên cùng một hệ trục tọa độ Oxy, vẽ đồ thị hai hàm số y=1/2x2(P) và y=-x+4(D).
b)Tìm tọa độ giao điểm M,N của (P) và(D) bằng phép tính.
Bài 4: Cho phương trình: x2 - 4x + m + 1= 0. Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn -x1x2 + (x1 + x2) = 2
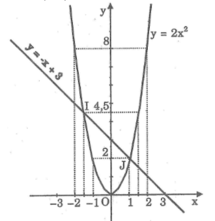
Giải phương trình bằng đồ thị : Cho phương trình 2 x 2 + x – 3 = 0.
Vẽ các đồ thị của hai hàm số y = 2 x 2 , y = -x + 3 trong cùng một mặt phẳng tọa độ.
*Vẽ đồ thị hàm số y = 2 x 2
| x | -2 | -1 | 0 | 1 | 2 |
| y = 2 x 2 | 8 | 2 | 0 | 2 | 8 |
*Vẽ đồ thị hàm số y = -x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 3 ⇒ (3; 0)
Vẽ đồ thị của hai hàm số y = 1 4 x 2 và y = - 1 4 x 4 trên cùng một hệ trục tọa độ.
Đường thẳng đi qua B(0; 4) và song song với trục Ox có dạng : y =4 .
Xét phương trình hoành độ giao điểm:
1 4 x 2 = 4 ⇔ x 2 = 16 ⇔ x = ± 4
Vậy hoành độ của M là x=-4 và M’ là x =4
- Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
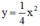 |
4 | 1 | 0 | 1 | 4 |
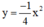 |
-4 | -1 | 0 | -1 | -4 |
- Vẽ đồ thị:
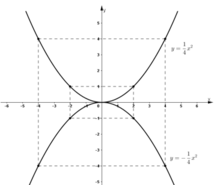
Đường thẳng qua B(0; 4) song song với Ox cắt đồ thị tại hai điểm M, M' (xem hình). Từ đồ thị ta có hoành độ của M là x = 4, của M' là x = - 4.
1) vẽ đồ thị của hai phương trình sau trên cùng một hệ trục rồi tìm tọa độ giao điểm của hai đồ thị: x + 2 y = 1 và -2 x + 4 y = -10
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)
1) vẽ đồ thị của hai phương trình sau trên cùng một hệ trục rồi tìm tọa độ giao điểm của hai đồ thị: x + 2 y = 1 và -2 x + 4 y = -10
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)
1) vẽ đồ thị của hai phương trình sau trên cùng một hệ trục rồi tìm tọa độ giao điểm của hai đồ thị: x + 2 y = 1 và -2 x + 4 y = -10
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\8y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-2y=3\\y=-1\end{matrix}\right.\)
Cho phương trình x2 - x - 2 = 0.
a) Giải phương trình.
b) Vẽ hai đồ thị y = x2 và y = x + 2 trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là x = -1; x= 2. Hai giá trị này cũng chính là nghiệm của phương trình x2 - x - 2 = 0 ở câu a).
cho parapol (P): y=x2 và đường thẳng (d): y=-x+2
a) vẽ đồ thị (P) và (d) trên cùng một hệ trục tọa độ
b) tìm tọa độ giao điểm của (d) và (P)
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\)(1)
a=1; b=1; c=-2
Vì a+b+c=0 nên phương trình (1) có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-2}{1}=-2\)
Thay x=1 vào (d), ta được:
y=-1+2=1
Thay x=-2 vào (d), ta được:
y=-(-2)+2=2+2=4
Vậy: (P) và (d) có hai tọa độ giao điểm là (1;1) và (-2;4)