Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x ( 2017 + 2019 - x 2 ) trên tập xác định của nó. Tính M-m.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = x(2017 +\(\sqrt{2019-x^2}\)) trên tập xác định của nó . Tính M-m
đây là đáp án
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 Tính M – m.
A. M - m = 2 2
B. M - m = 2 2 + 2
C. M-n=4
D. M - n = 2 2 - 2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 . Tính M – m.
A. M - m = 2 2
B. M - m = 2 2 + 2
C. M - m = 4
D. M - m = 2 2 - 2
Chọn B.
Phương pháp
- Tính y' , tìm các nghiệm của y' = 0 .
- Tính giá trị của hàm số tại các điểm đầu mút và các điểm vừa tìm được ở bước trên và so sánh kết quả.
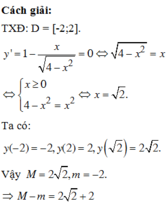
Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 . Giá trị của biểu thức (M + 2N) là
A. 2 2 + 2
B. 4 - 2 2
C. 2 2 - 4
D. 2 2 - 2
Chọn C
Tập xác định của hàm số: D = [-2;2]
Ta có 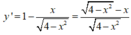
![]()
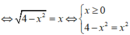
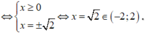
Ta lại có ![]()
Từ đó suy ra ![]()
Vậy ![]()
Gọi M,N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 Giá trị của biểu thức M + 2 N là
A. 2 2 + 2
B. 4- 2 2
C. 2 2 -4
D. 2 2 -2
Chọn C.
Tập xác định của hàm số ![]()
Cách 1: Bấm máy tính. Với máy 580vn chọn start:-2, end: 2, step: 2/9 có: ![]()
thử thấy phương án C gần nhất với kết quả này nên ta chọn C.
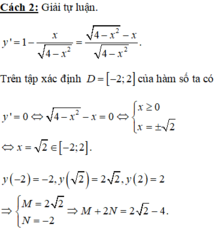
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 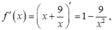
![]()
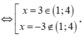
Có ![]()
![]()
Vậy m + M = 16.
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn 1 , 4 . Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + x + 1 . Giá trị của M - 3m bằng bao nhiêu?
A. 0
B. 1
C. -1
D. 2