Các câu hỏi tương tự
Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = x(2017 +\(\sqrt{2019-x^2}\)) trên tập xác định của nó . Tính M-m
Cho hàm số y = f(x) xác định và liên tục trên R có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số. Giá trị của M – m bằng
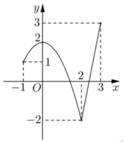
A. 0.
B. 1.
C. 4.
D. 5.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
x
2
+
x
+
3
x
-
2
trên [-2;1] . Tính TM+2m .
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= x 2 + x + 3 x - 2 trên [-2;1] . Tính T=M+2m .
![]()
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 1 x trên [ 1 3 ; 3 ) Tính 3M+2m
A. 13 6
B. 15
C. 14
D. 12
Cho hàm số
y
f
x
xác định và liên tục trên R có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
y
f
-
sin
x
+
2
. Giá trị c...
Đọc tiếp
Cho hàm số y = f x xác định và liên tục trên R có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f - sin x + 2 . Giá trị của M – m bằng
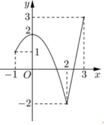
A. 0
B. 1
C. 4
D. 5
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
x
+
4
-
x
2
Tính M – m. A.
M
-
m
2
2
B.
M
-
m
2
2
+
2
C. M-n4 D.
M
-
n
2
2...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 Tính M – m.
A. M - m = 2 2
B. M - m = 2 2 + 2
C. M-n=4
D. M - n = 2 2 - 2
Cho hàm số y=f(x) liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2]. Tính M + m.
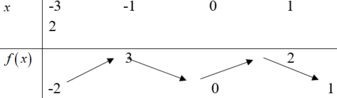
A. 3
B. 2
C. 1
D. 4






