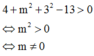rong không gian với hệ trục tọa độ Oxyz, tìm tất cả giá trị của m để phương trình x 2 + y 2 + z 2 - 2 m + 2 + 4 m y + 19 m - 6 = 0 là phương trình mặt cầu.
A. 1 < m < 2
B. m < 1 h o ặ c m > 2
C. - 2 ≤ m ≤ 1
D. m < - 2 h o ặ c m > 1
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, tìm tất cả các giá trị của m để phương trình
x
2
+
y
2
+
z
2
-
2
m
+
1
y
+
4
z
+
8
0
là phương trình mặt cầu. A.
-
1
-
2
15...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, tìm tất cả các giá trị của m để phương trình x 2 + y 2 + z 2 - 2 m + 1 y + 4 z + 8 = 0 là phương trình mặt cầu.
A. - 1 - 2 15 < m < - 1 + 2 15
B. m > - 1 + 2 15 h o ặ c m < - 1 - 2 15
C. -3 < m < 1
D. m < - 3 h o ặ c m > 1
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình
x
6
+
t
y
-
2
-
5
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu số tự nhiên của tham số m để phương phương trình
x
2
+
y
2
+
z
2
+
2
(
m
-
2
)
y
-
2
(...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu số tự nhiên của tham số m để phương phương trình x 2 + y 2 + z 2 + 2 ( m - 2 ) y - 2 ( m + 3 ) z + 3 m 2 + 7 = 0 là phương trình của một mặt cầu.
A. 2
B. 3
C. 4
D. 5
Đáp án là C.
Để phương trình đã cho là phương trình mặt cầu thì
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng
d
1
:
x
+
1
2
1
-
y
-
m
2
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d 1 : x + 1 2 = 1 - y - m = 2 - z - 3 và d 2 : x - 3 1 = y 1 = z - 1 1 . Tìm tất cả các giá trị thực của m để d 1 ⊥ d 2 được:
A. -1
B. 1
C. -5
D. 5
Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu giá trị của tham số
m
∈
N
để phương trình
x
2
+
y
2
+
z
2
+
2
m...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu giá trị của tham số m ∈ N để phương trình x 2 + y 2 + z 2 + 2 m - 2 y - 2 m + 3 z + 3 m 2 + 7 = 0 là phương trình của một mặt cầu ?
A. 2.
B. 3.
C. 4.
D. 5
Chọn đáp án C.
Ta có
Phương trình x 2 + y 2 + z 2 + 2 m - 2 y - 2 m + 3 z + 3 m 2 + 7 = 0
là phương trình của một mặt cầu khi a 2 + b 2 + c 2 - d > 0
Do m ∈ N nên m ∈ 0 ; 1 ; 2 ; 3
Vậy có 4 giá trị m ∈ N thỏa mãn bài toán
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị m để phương trình
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
4
z
+
m
0
là phương trình của một mặt cầu.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị m để phương trình x 2 + y 2 + z 2 - 2 x - 2 y - 4 z + m = 0 là phương trình của một mặt cầu.
Trong không gian với hệ trục tọa độ Oxyz, tìm tất cả giá trị thực của tham số m để đường thẳng
d
:
x
-
2
-
2
y
-
1
1
z
1
song song với mặt phẳng
P
:
2
x
+...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, tìm tất cả giá trị thực của tham số m để đường thẳng d : x - 2 - 2 = y - 1 1 = z 1 song song với mặt phẳng P : 2 x + 1 - 2 m y + m 2 z + 1 = 0 .
A. m ∈ - 1 ; 3
B. m=3
C. Không có giá trị nào của m
D. m=-1
Trong không gian với hệ tọa độ Oxyz cho
S
:
x
-
2
2
+
y
-
1
2
+
z
+
1
1
1
là phương trình mặt cầu và...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho S : x - 2 2 + y - 1 2 + z + 1 1 = 1 là phương trình mặt cầu và P : 3 x - 2 y + 6 z + m = 0 là phương trình mặt phẳng. Tìm tất cả các giá trị thực của m để mặt cầu (P) và mặt phẳng có điểm chung.
A. m > 3; m < 2
B. 2 ≤ m ≤ 3
C. - 5 ≤ m ≤ 9
D. m > 9; m < -5
Mặt cầu (S) có tâm I(2;1;-1) và bán kính R = 1
Mặt cầu (S) và mặt phẳng (P) có điểm chung với nhau khi và chỉ khi
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của tham số m để phương trình
x
2
+
y
2
+
z
2
-
4
x
+
2
m
y
+
6
z
+
13
0
là phương trình của mặt cầu.
Đọc tiếp
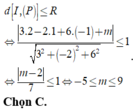
Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của tham số m để phương trình x 2 + y 2 + z 2 - 4 x + 2 m y + 6 z + 13 = 0 là phương trình của mặt cầu.
Đáp án B.
Để phương trình x 2 + y 2 + z 2 - 4 x + 2 m y + 6 z + 13 = 0 là phương trình của mặt cầu thì
Đúng 0
Bình luận (0)