Cho số phức z = 2 - 3 i . Môđun của số phức w = 1 + i z
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
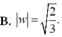
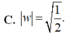
![]()
Cho số phức 2-3i. Môđun của số phức w=(1+i)z bằng
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức 2 – 3i. Môđun của số phức w = (1+i)z bằng
A. w = 26
B. w = 37
C. w = 5
D. w = 4
Cho số phức 2 - 3i Môđun của số phức w = (1 + i)z bằng
![]()
![]()
![]()
![]()
Cho số phức z=1-i. Tính môđun của số phức w = z - - 2 i z - 1
A. w = 2
B. w = 1
C. w = 2
D. w = 3
Cho số phức z = 1 − i . Tính môđun của số phức w = z ¯ − 2 i z − 1 .
A. w = 2
B. w = 1
C. w = 2
D. w = 3
Cho số phức z=1+i. Tính môđun của số phức w = z ¯ + 2 i z − 1 .
A. 2
B. 1
C. 0
D. 2
Cho số phức z( 3 - 2i)(1 + i) 2 . Môđun của w = i z + z ¯ là
A.2.
B. 2 2
C. 1.
D. 2
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .