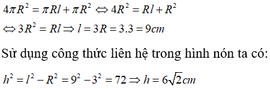Cho mặt cầu có diện tích bằng 8 π a 2 3 , bán kính của mặt cầu bằng
A. a 6 3
B. a 3 3
C. a 6 2
D. a 2 3
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Chọn C.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là: S = 4 π R 2 .
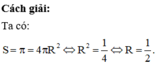
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng:
![]()
![]()
Cho mặt cầu có diện tích bằng 8 πa 2 3 , bán kính của mặt cầu bằng

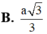

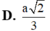
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Một mặt cầu có bán kính bằng 2 có diện tích mặt cầu bằng
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính đáy là 4cm . Một hình cầu có diện tích mặt cầu bằng diện tích hai đáy của hình trụ.Tính bán kính hình cầu?
A. R = 3cm
B. R = 4cm
C. R = 2 2 cm
D. R = 3 2 cm
Cho một mặt cầu có diện tích bằng 8 πa 2 3 . Tính bán kính mặt cầu.
A. a 6 3
B. a 6 5
C. a 6 7
D. a 6 15
Cho mặt cầu có diện tích bằng 8 πa 2 3 Tính bán kính mặt cầu đó
A . a 3 3
B . a 2 3
C . a 6 3
D . 2 a 6 3
Cho hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón:
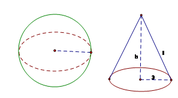
A. 3
B. 6 3
C. 72
D. 6 2
Đáp án D
Gọi l là độ dài đường sinh của hình nón.
Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có: