Tìm tất cả các giá tri thực của tham số m để bất phương trình 2 3 x + m − 1 3 x + m − 1 > 0 nghiệm đúng với mọi x ∈ ℝ
A. m ∈ ℝ
B. m > 1
C. m ≤ 1
D. m ≥ 1
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
Tìm tất cả các giá tri thực của tham số m để phương trình log 2 2 x + log 2 x + m = 0 có nghiệm thực x ∈ 0 ; 1 là:
![]()
![]()
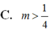
![]()
Tìm tất cả các giá trị thực của tham số m để bất phương trình -2x2 +2(m-2)x+m-2<0 có nghiệm
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
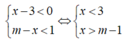
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 5 x - 1 . log 2 2 . 5 x - 2 ≥ m có nghiệm x ≥ 1
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Đáp án C.
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m
Đặt t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )
Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m
Với f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0 với t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6
Do đó theo bài ra để bất phương trình có nghiệm x ≥ 1 thì m ≤ min f ( t ) ⇔ m ≤ 6
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m (m là tham số). Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi x > 1
A. m > 1
B. m ≥ 1
C. m > 5 4
D. m ≥ 5 4
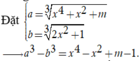
Khi đó bất phương trình trở thành
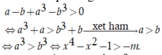
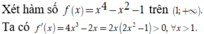
Suy ra hàm số f(x) đồng biến trên ![]()
Do đó yêu cầu bài toán ![]()
Chọn B.
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 1 2 x - 1 > log 1 2 x 3 + x - m có nghiệm
A. mÎR
B. m < 2
C. m ≤ 2
D. Không tồn tại m