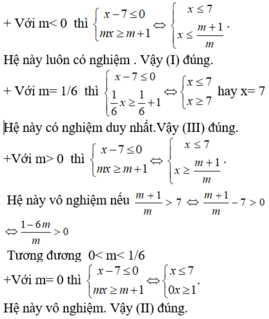Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm? 0 x + 3 y = - 8 0 x - 21 y = 56

Những câu hỏi liên quan
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm?
2
x
+
0
y
5
4
x
+
0
y...
Đọc tiếp
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm? 2 x + 0 y = 5 4 x + 0 y = 7
Đường thẳng 2x + 0y = 5 ⇔ x = 2,5 song song với trục tung
Đường thẳng 4x + 0 y = 7 ⇔ x = 1,75 song song với trục tung nên chúng cũng song song với nhau.
Vậy hệ
2
x
+
0
y
=
5
4
x
+
0
y
=
7
vô nghiệm
Đúng 0
Bình luận (0)
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm?
0
x
+
3
y
-
8
0
x
-
21
y...
Đọc tiếp
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm? 0 x + 3 y = - 8 0 x - 21 y = 50
Đường thẳng 0x + 3y = -8 là đường thẳng y = -8/3 song song với trục hoành
Đường thẳng 0 x - 21 y = 50 ⇔ y = - 50 21 là đường thẳng song song với trục hoành nên chúng song song với nhau.
Hệ
0
x
+
3
y
=
-
8
0
x
-
21
y
=
50
vô nghiệm.
Đúng 0
Bình luận (0)
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm?
2
x
+
0
y
5
4
x
+
0
y
10
Đọc tiếp
Những hệ phương trình nào sau đây vô nghiệm, những hệ nào có vô số nghiệm? 2 x + 0 y = 5 4 x + 0 y = 10
Đường thẳng 2x + 0y = 5 và đường thẳng 4x + 0y = 10 trùng nhau
Vậy hệ
2 x + 0 y = 5 4 x + 0 y = 10
Vô số nghiệm
Đúng 0
Bình luận (0)
Hệ phương trình nào sau đây có vô số nghiệm: A.
x
-
3
y
6
-
1
3
x
+
y...
Đọc tiếp
Hệ phương trình nào sau đây có vô số nghiệm:
A. x - 3 y = 6 - 1 3 x + y = - 2
B. x - 3 y = 5 - 1 3 x + y = - 2
C. x - 3 y = 6 - 1 3 x - y = 2
D. x - 3 y = 5 1 3 x + y = - 2
Chọn đáp án A
Xét hệ phương trình: 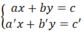 Nếu ta có:
Nếu ta có:
TH 1: 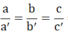 ⇒ hpt có vô số nghiệm
⇒ hpt có vô số nghiệm
TH 2: 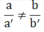 ⇒ hpt có 1 nghiệm duy nhất
⇒ hpt có 1 nghiệm duy nhất
TH 3: 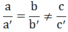 ⇒ hpt vô nghiệm
⇒ hpt vô nghiệm
Đúng 0
Bình luận (0)
Cho hệ bất phương trình
x
-
7
≤
0
mx
≥
m
+
1
Xét các mệnh đề sau : (1) : Với m 0 , hệ luôn có nghiệm. (2) : Với 0 ≤ m 1/6 hệ vô nghiệm. (3) : Với m 1/6 hệ có nghiệm duy nhất. Mệ...
Đọc tiếp
Cho hệ bất phương trình x - 7 ≤ 0 mx ≥ m + 1
Xét các mệnh đề sau :
(1) : Với m< 0 , hệ luôn có nghiệm.
(2) : Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) : Với m = 1/6 hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D. (1) ; (2) và (3)
Cho hệ bất phương trình
x
-
7
≤
0
m
x
≥
m
+
1
. Xét cá...
Đọc tiếp
Cho hệ bất phương trình x - 7 ≤ 0 m x ≥ m + 1 . Xét các mệnh đề sau
(1) Với m< 0 , hệ luôn có nghiệm.
(2) Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) Với m= 1/6 , hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D . Cả ba đúng
Với giá trị nào của k thì hệ phương trình sau đây:\(\hept{\begin{cases}x+ky=3\\kx+4y=6\end{cases}}\)
a,Có nghiệm duy nhất
b,Có vô số nghiệm?
c,Vô nghiệm?
\(\hept{\begin{cases}x+ky=3\\kx+4y=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3-x}{k}\left(k\ne0\right)\\kx+4.\frac{3-x}{k}=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{3-x}{k}\\\frac{k^2x+12-4x}{k}=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}k^2x+12-4x-6k=0\\y=\frac{3-x}{k}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x\left(k^2-4\right)-6\left(k-2\right)=0\\y=\frac{3-x}{k}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(k-2\right)\left[x\left(k+2\right)-6\right]=0\\y=\frac{3-x}{k}\end{cases}}\)
a, Với \(k\ne2\)thì Pt có nghiệm là \(x=\frac{6}{k+2}\)
Vậy Pt có nghiệm duy nhất : \(x=\frac{6}{k+2};y=\frac{3-\frac{6}{k+2}}{k}=\frac{3k}{k}=3\)
b,Với \(k=2\)thì pt có vô số nghiệm
ms lp 8 , có chi thông cảm
Đúng 0
Bình luận (0)
x+ky=3
=> x=3-ky thế vào phương trình thứ 2
=> k( 3-ky)+4y=6 <=> \(\left(4-k^2\right)y=6-3k\) (3)
+) \(4-k^2=0\Leftrightarrow k=\pm2\)
Với k=2, phương trình 3 trở thành: 0.y=0 => phương trình có vô số nghiệm => hệ ban đầu có vô số nghiệm
Với k=-2, phương trình (3) trở thành: 0.y=12 => phương trình vô nghiệm => hệ ban đầu vô nghiệm
+) \(k\ne\pm2\)Phương trình (3) <=> y=\(\frac{3}{2+k}\)=> x=3-ky=\(3-\frac{3k}{k+2}=\frac{6}{k+2}\)
Hệ phương trình có nghiệm duy nhất (x, y) tương ứng như trên
Kết luận
a) k khác 2, -2
b) k=2
c) k =-2
Đúng 0
Bình luận (0)
Hệ phương trình nào sau đây vô nghiệm? A.
4
x
+
3
1
x
+
2
y
0
. B....
Đọc tiếp
Hệ phương trình nào sau đây vô nghiệm?
A. 4 x + 3 = 1 x + 2 y = 0 .
B. x + y = 3 - x - y = - 3 .
C. x + y = 1 x - 2 y = 0
D. - x + y = 0 2 x - 2 y = - 6
Đáp án D
Cách 1: Dùng máy tính cầm tay nhận thấy hệ phương trình - x + y = 0 2 x - 2 y = - 6 vô nghiệm
Cách 2: Chỉ có đáp án D có - 1 2 = 1 - 2 ≠ 0 6 suy ra hệ phương trình vô nghiệm
Đúng 0
Bình luận (0)
Hệ phương trình nào sau đây vô nghiệm: A.
x
-
3
y
6
-
1
3
x
+
y...
Đọc tiếp
Hệ phương trình nào sau đây vô nghiệm:
A. x - 3 y = 6 - 1 3 x + y = - 2
B. x - 3 y = 5 1 3 x + y = - 2
C. x - 3 y = 6 1 3 x - y = - 2
D. x - 3 y = 5 - 1 3 x - y = - 2