Cho hình hộp chữ nhật ABCD.A'B'C'D'.Chứng minh rằng
a) BDD'B' là hình chữ nhật
b) BB' vuông góc với mặt phẳng (ABCD)
c) mặt phẳng (ABB'A') vuông góc với mặt phẳng (ABCD)
giải giúp mình nhé mình tick cho
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy ABCD là hình vuông, chiều cao AA' = a và A ' C A ^ = 45 ° . Hãy tính:
a) Diện tích toàn phần hình hộp theo a;
b) Thể tích hình hộp theo a
Câu 21: Cho khối hộp chữ nhật ABCD.A'B'C'D'. Biết AC=5, AB'=7, AD'=8. Tính thể tích khối hộp chữ nhật này?
Câu 36: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, \(AD=a\sqrt{3}\). SA\(\perp\)(ABCD), SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với cạnh bên SC, cắt các cạnh bên SB,SC,SD lần lượt tại E,F,H. Tính thể tích khối chóp S.AEFH?
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có các kích thước là a , b , c ( a < b < c ) . Hình hộp chữ nhật này có mấy mặt đối xứng
A. 1
B. 2
C. 3
D. 4
Chọn C.
Hình hộp chữ nhật ABCD.A’B’C’D’ có 3 mặt đối xứng, đó là các mặt phẳng trung trực AB, AD, AA’.
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a 3 . Hình chiếu vuông góc với B' trên mặt phẳng (ABCD) là trung điểm AC, mặt phẳng (CDD'C') tạo với đáy góc 60 0 .Tính theo a thể tích khối hộp ABCD.A'B'C'D'
A . 9 a 3 8
B . a 3 8
C . 27 a 3 8
D . 2 a 3 3 9
Đáp án C.
Chú ý
∆
ABC đều cạnh
a
3
. Kẻ OH
⊥
AB 
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy ABCD là hình vuông, AB=20cm, AA'=19,4cm.
a) Chứng minh tứ giác ABC'D', CDA'B' là hình chũ nhật
b) Tính thể tích và diện tích toàn phần của hình hộp.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
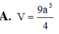
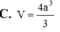
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
