Biết rằng tập hợp tất cả các điểm trên mặt phẳng toạ độ Oxy biểu diễn số phức z thoả mãn 3 z + z ¯ + 4 z - z ¯ = 24 là các cạnh của một hình thoi (H). Diện tích của (H) bằng
A. 48.
B. 24.
C. 16.
D. 32.
Tập hợp tất cả các điểm trong mặt phẳng toạ độ Oxy biểu diễn số phức z thoả mãn z - 1 + 2 i = z + 3 là đường thẳng có phương trình
![]()
![]()
![]()
![]()
Biết rằng tập hợp tất cả các điểm trên mặt phẳng toạ độ Oxyz biểu diễn số phức z thoả mãn 3 z + z ¯ + 4 z - z ¯ = 24 là các cạnh của một hình thoi (H). Diện tích của (H) bằng
A. 48
B. 24
C. 16
D. 32
Đặt ![]()
![]()
Đây là các cạnh của hình thoi ABCD có các đỉnh xác định bởi
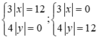
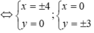
⇒ A(-4;0), B(0;3), C(4;0), D(0;-3)
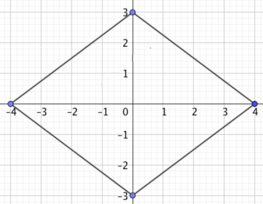
Và
![]()
Chọn đáp án B.
Xét các số phức z thoả mãn z ¯ - 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 13
B. 11
C. 11 2
D. 13 2
Xét các số phức z thoả mãn z ¯ + 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A . 13
B . 11
C. 11 2
D. 13 2
Trong mặt phẳng toạ độ Oxy tập hợp tất cả các điểm biểu diễn số phức z sao cho z 2 là số thuần ảo là
A. Hai đường thẳng y=x,y=-x nhưng bỏ đi điểm O(0;0)
B. Hai đường thẳng y=x,y=-x
C. Trục hoành và trục tung
D. Trục hoành và trục tung nhưng bỏ điểm O(0;0)
Đặt ![]()
![]() thuần ảo
⇔
phần thực bằng
thuần ảo
⇔
phần thực bằng 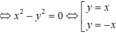 Vậy tập hợp tất cả các điểm biểu diễn số phức z là hai đường thẳng y=x;y=-x
Vậy tập hợp tất cả các điểm biểu diễn số phức z là hai đường thẳng y=x;y=-x
Chọn đáp án B.
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - 3 - 4 i = 2
A. Đường tròn tâm I(3;4) bán kính R = 2
B. Đường tròn tâm I(3;4) bán kính R=2
C. Đường tròn tâm I(3;-4) bán kính R = 2
D. Đường tròn tâm I(3;-4) bán kính R=2
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - ( 3 - 4 i ) = 2
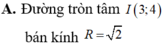
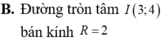
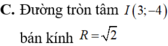
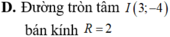
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
A. Đường tròn ( x - 2) 2 + ( y + 2) 2 = 100.
B. Elip 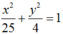
C. Đường tròn ( x -2) 2 + ( y + 2) 2 = 10.
D. Elip 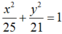
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là ![]()
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình 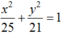
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 1 ≤ z ≤ 2 là một hình phẳng tích bằng
A. 4 π
B. 3 π
C. π
D. 2 π