Đặt ![]()
![]()
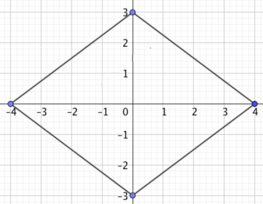
Đây là các cạnh của hình thoi ABCD có các đỉnh xác định bởi
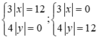
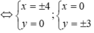
⇒ A(-4;0), B(0;3), C(4;0), D(0;-3)
Và
![]()
Chọn đáp án B.
Đặt ![]()
![]()
Đây là các cạnh của hình thoi ABCD có các đỉnh xác định bởi
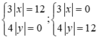
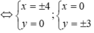
⇒ A(-4;0), B(0;3), C(4;0), D(0;-3)

Và
![]()
Chọn đáp án B.
Xét các số phức z thoả mãn z ¯ - 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 13
B. 11
C. 11 2
D. 13 2
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 1 ≤ z ≤ 2 là một hình phẳng tích bằng
A. 4 π
B. 3 π
C. π
D. 2 π
Xét các số phức z thỏa mãn z - + 1 + 3 i = 2 z - 1 . Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng
A. 11
B. 5
C. 5
D. 11
Xét các điểm số phức z thỏa mãn z ¯ + i z + 2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng:
A. 1.
B. 5 4
C. 5 2
D. 3 2
Xét các số phức z thỏa mãn z ¯ - 2 i z + 2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng?
A. 2 2
B. 2
C. 2
D. 4
Cho số phức z thỏa mãn điều kiện z + 4 + z - 4 = 10 Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là một hình phẳng có diện tích bằng
A. 20 π
B. 15 π
C. 12 π
D. 16 π
Tập hợp tất cả các điểm biểu diễn số phức z thoả mãn z 2 + z + z ¯ = 0 là một đường tròn, diện tích giới hạn bởi đường tròn đó bằng
A. 4 π
B. 2 π
C. 3 π
D. π
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z = z - 3 + 4 i là đường thẳng
A. 2 x - 3 = 0
B. 6 x - 8 y - 25 = 0
C. 6 x + 8 y - 25 = 0
D. y - 2 = 0
Cho số phức z thoả mãn z - 1 ≤ 1 và z - z ¯ có phần ảo không âm. Tập hợp các điểm biểu diễn số phức z là một miền phẳng. Tính diện tích S của miền phẳng này
A. S = π
B. S = 2 π
C. S = 1 2 π
D.S = 1.