tim x :
a) I x+1I+I x -2I+I x+3I = 6
b) 2Ix+2I+I4-xi= 11
c) IxI - I 2x+3I = x-1
tim x :
a) I x+1I+I x -2I+I x+3I = 6
b) 2Ix+2I+I4-xi= 11
c) IxI - I 2x+3I = x-1
tim x :
a) I x+1I+I x -2I+I x+3I = 6
b) 2Ix+2I+I4-xi= 11
c) IxI - I 2x+3I = x-1
Bài 1 : lập bảng xét dấu để bỏ giá trị tuyệt đối .
A ) I3x-1I + Ix-1I = 4
C ) I x-2I + Ix-3I + Ix-4I = 2
D ) 2 x Ix+2I + I4-xI = 11
Làm mẫu 1 phần :
a) \(|3x-1|+|x-1|=4\left(1\right)\)
Ta có: \(3x-1=0\Leftrightarrow x=\frac{1}{3}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
+) Với \(x< \frac{1}{3}\Rightarrow\hept{\begin{cases}3x-1< 0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=1-3x\\|x-1|=1-x\end{cases}\left(2\right)}}\)
Thay (2) vào (1) ta được :
\(\left(1-3x\right)+\left(1-x\right)=4\)
\(2-4x=4\)
\(4x=-2\)
\(x=\frac{-1}{2}\)( chọn )
+) Với \(\frac{1}{3}\le x< 1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(3x-1\right)+\left(1-x\right)=4\)
\(2x=4\)
\(x=2\)( chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}3x-1>0\\x-1>0\end{cases}\Rightarrow}\hept{\begin{cases}|3x-1|=3x-1\\|x-1|=x-1\end{cases}\left(4\right)}\)
Thay (4) vào (1) ta được :
\(\left(3x-1\right)+\left(x-1\right)=4\)
\(4x-2=4\)
\(4x=6\)
\(x=\frac{3}{2}\)( chọn )
Vậy \(x\in\left\{\frac{-1}{2};2;\frac{3}{2}\right\}\)
Giải các pt sau:
a) I2x-5I = I3-8xI
b) I4x-3I = 5-2x
c) Ix+1I+Ix+2I = I4-xI+I5-xI
d) Ix-3I-2Ix-2I+3Ix-1I=0
Các bạn giúp mk với ạ:33
a: \(\Leftrightarrow\left[{}\begin{matrix}2x-5=3-8x\\2x-5=8x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}10x=8\\-6x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
a) -Ix+1I+Ix+2I=x-1
b) Ix-3I- I 2x+1I
Tính x
a, I 3x-2I<4
b, I3-2xI<x+1
c, I3x-1I>5
d, I3x+1I>I x-2I
e, I x-1I> I x+2I -3
g, Ix-1I+Ix+5I>8
h, Ix-3I +Ix+1I<8
a: \(\Leftrightarrow\left\{{}\begin{matrix}3x-2>-4\\3x-2< 4\end{matrix}\right.\Leftrightarrow-\dfrac{2}{3}< x< 2\)
c: \(\Leftrightarrow\left[{}\begin{matrix}3x-1>5\\3x-1< -5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>2\\x< -\dfrac{4}{3}\end{matrix}\right.\)
d: \(\Leftrightarrow\left[{}\begin{matrix}3x+1>x-2\\3x+1< -x+2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x>-3\\4x< 1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-\dfrac{3}{2}\\x< \dfrac{1}{4}\end{matrix}\right.\)
Giải các phương trình sau trên tập số phức:
a) (3 + 4i)x = (1 + 2i)(4 + i)
b) 2ix + 3 = 5x + 4i
c) 3x(2 – i) + 1 = 2ix(1 + i) + 3i
a) (3 + 4i)x = (1 + 2i)(4 + i)
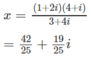
b) 2ix + 3 = 5x + 4i
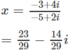
c) 3x(2 – i) + 1 =2ix(1 + i) + 3i
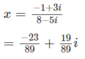
bài 1 : Lập bảng xét dấu để bỏ giá trị tuyệt đối
a ) I3x-1I + Ix-1I = 4
b ) Ix-2I + Ix-3I + Ix-4I = 2
C ) IX+1I + Ix-2I + Ix-3I = 6
d ) 2 x Ix+2I + I4-xI = 11
Tìm giá trị nhỏ nhất của biểu thức sau:
B=I x-1I + I x-2I + Ix-3I + 2011Ta có:
\(B-2011=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|\)
\(\ge x-1+0+3-x=2\)
\(\Rightarrow B-2011\ge2\)\(\Rightarrow B\ge2013\)
Dấu = khi \(\begin{cases}x-1\ge0\\x-2=0\\3-x\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge1\\x=2\\x\le3\end{cases}\)\(\Leftrightarrow x=2\)
Vậy MinB=2013 khi x=2