Ba số x,y,x (y>0) theo thứ tự lập thành một cấp số cộng tăng. Giả sử x 2 , y 2 , z 2 theo thứ tự đó lập thành một cấp số nhân. Khi đó công bội của cấp số nhân đó bằng
A. 2 - 1
B. 2 + 1
C. 3 - 2 2
D. 3 + 2 2
Ba số x , y , z ( y > 0 ) theo thứ tự lập thành một cấp số cộng tăng. Giả sử x 2 , y 2 , z 2 theo thứ tự đó lập thành một cấp số nhân. Khi đó công bội của cấp số nhân đó bằng
A. 2 - 1
B. 2 + 1
C. 3 - 2 2
D. 3 + 2 2
Có bao nhiêu cặp số thực (x;y) thỏa mãn: ba số 4x-2y, 3x+y, x+6y theo thứ tự lập thành một cấp số cộng và ba số (y+2)2, xy-1, (x+1)2 theo thứ tự lập thành cấp số nhân
A. 1
B. 2
C. 3
D. 0
Ba số x, y, z theo thứ tự lập thành một cấp số nhân có công bội q ≠ 1 . Đồng thời , các số x , 2 y , 3 z theo thứ tự đó lập thành một cấp số cộng có công sai khác 0. Khi đó công bội q bằng
A. - 1 3
B. 3
C. 1 3
D. -3
Ba số x, y, z theo thứ tự lập thành một cấp số nhân có công bội q ≠ 1 . Đồng thời, các số x, 2y, 3z theo thứ tự đó lập thành một cấp số cộng có công sai khác 0. Khi đó công bội q bằng:
A. - 1 3
B. 3
C. 1 3
D. -3
Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 ; đồng thời các số x ; 2y ; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q.
A. q = 1 3 .
B. q = 1 9 .
B. q = − 1 3 .
D. q = − 3.
Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2
A. F = 389 hoặc F = 179
B. F = 441 hoặc F = 357
C. F = 395 hoặc F = 179
D. F = 389 hoặc F = 395
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2 .
A. F = 389 hoặc F = 179
B. F = 441 hoặc F = 357
C. F = 395 hoặc F = 179
D. F = 389 hoặc F = 395
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
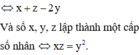
Cách giải:
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
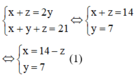
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân nên ta có:
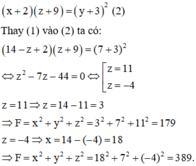
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2 ; 3 ; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2 .
A. F=389 Hoặc F=395
B.F=395 Hoặc F=179
C.F=389 Hoặc F=179
D.F=441 Hoặc F=357
Chọn C
*Theo tính chất của cấp số cộng , ta có x+ z = 2y.
Kết hợp với giả thiết, x+ y + z = 21, ta suy ra 3y = 21 nên y = 7.
* Gọi d là công sai của cấp số cộng thì x = y − d = 7 − d và z = y + d = 7 + d .
Sau khi thêm các số 2 ; 3 ; 9 vào ba số x ; y ; z ta được ba số là x+ 2 ; y + 3 ; z + 9 hay
9- d ; 10 ; 16+ d.
* Theo tính chất của cấp số nhân, ta có
9 − d 16 + d = 10 2 ⇔ d 2 + 7 d − 44 = 0
Giải phương trình ta được d= -11 hoặc d= 4.
Với d = -11 ; cấp số cộng 18 ; 7 ; - 4. Lúc này F = 389.
Với d= 4, cấp số cộng 3 ; 7 ; 11. Lúc này F = 179.
Bài 1 : Ba số 5x - y ; 2x + 1 và x - y theo thứ tự lập thành Cấp số cộng . Ba số 3;căn(2x + y) và x + 1 theo thứ tự lập thành Cấp số nhân . Tìm x,y
5x-y;2x+1;x-y lập thành cấp số cộng nên
5x-y+x-y=2(2x+1)
=>6x-2y=4x+2
=>2x-2y=2
=>x-y=1
=>y=x-1
\(3;\sqrt{2x+y};x+1\) lập thành cấp số nhân thì \(\left(\sqrt{2x+y}\right)^2=3\left(x+1\right)\)
=>\(2x+y=3x+3\) hoặc -2x-y=3x+3
=>2x+x-1=3x+3 hoặc -2x-x+1=3x+3
=>-1=3(loại) hoặc -3x+1=3x+3
=>-6x=2
=>x=-1/3
=>y=-1/3-1=-4/3
Thử lại, ta sẽ thấy: 2x+y=-2/3-4/3=-6/3=-2<0
=>\(\sqrt{2x+y}\) không có giá trị
Vậy: Không có cặp số (x,y) nào thỏa mãn đề bài