Cho F(x) là một nguyên hàm của f(x) = 2x + 1 trên R. Biết hàm số y = F(x) đạt giá trị nhỏ nhất bằng  39 4 . Đồ thị của hàm số y = F(x) cắt trục tung tại điểm có tung độ là

A.  10

B.  11

C.  37 4

D.  39 4

Cho F(x) là một nguyên hàm của hàm số f(x)=|1+x|-|1-x| trên tập R và thỏa mãn F(1)= 3.Tính tổng F(0)+F(2)+F(-3).

Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x), biết  ∫ 0 9 f x d x = 9  và F(0) = 9.

A. F(9) = -3

B. F(9) = -12.

C. F(9) = 12.

D. F(9) = 6.

Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x) biết ∫ 0 9 f x d x = 9  và F(0)=9

A. F(9) = -3

B. F(9) = -12

C. F(9) = 12

D. F(9) = 6

Cho hàm số f(x) liên tục trên R+ và thoả mãn  ∫ f ( x + 1 ) x + 1 d x   =   2 ( x + 1 + 3 ) x + 5 + C   . Nguyên hàm của hàm số f(2x) trên tập R+ là

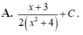
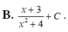
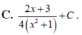
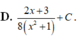
Biết  F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số  f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng

A. 9e

B. 3e

C.  20 e 2

D.  - 1 e